Eigenfrequenz

Eine Eigenfrequenz eines schwingfähigen Systems ist eine Frequenz, mit der das System nach einmaliger Anregung als Eigenform schwingen kann.

Für eine kreisförmige stehende Welle muss ein ganzzahliges Verhältnis Umfang/Wellenlänge vorliegen. Es gibt immer mehrere Eigenfrequenzen.

Wenn einem solchen System von außen Schwingungen aufgezwungen werden, deren Frequenz mit der Eigenfrequenz übereinstimmt, reagiert das System mit besonders großen Amplituden, was man als Resonanz oder, wenn zerstörende Auswirkungen auftreten, Resonanzkatastrophe bezeichnet.

Freiheitsgrade

Man schreibt einen System so viele Freiheitsgrade zu, als es voneinander unabhängige Bewegungsmöglichkeiten besitzt.

„Man wird dann sehen, dass solche Systeme immer eine Zahl an Eigenfrequenzen besitzen, die der Zahl der Freiheitsgrade entspricht^[1] “

– Horst Irretier

Ein Freiheitsgrad beim Federpendel

Wie die Eigenfrequenz eines Systems mit nur einem Freiheitsgrad bestimmt wird, kann am Beispiel eines Federpendels erklärt werden. Eine Kugel mit der Masse m hängt an einer Schraubenfeder mit der federspezifischen Konstante c. Diese ist definiert als Kraft pro Auslenkung, mit der die Feder reagiert. Die Kugel unterliegt dem Zweiten Newton'schen Axiom (Masse * Beschleunigung = Summe aller Kräfte, die auf die Kugel wirken). Die statischen Kräfte in der Ruhelage sind für sich alleine in der Summe Null, also kann das Gewicht und die statische Federkraft ignoriert werden. Übrig bleibt eine Abweichung von der statischen Federkraft als einzige Kraft, die zu berücksichtigen ist. Diese Kraft zieht die Kugel nach oben, wenn diese sich unterhalb der Ruhelage befindet und drückt die Kugel nach unten, wenn diese sich oberhalb der Ruhelage befindet. Also ist Masse * Beschleunigung entgegengesetzt gleich dem c-fachen der Auslenkung z(t), die mit der Zeit t schwankt:

$m \ddot z = - c z(t) \Rightarrow m \ddot z + c z(t) = 0$

Diese lineare homogene Differentialgleichung lässt sich mit folgendem Ansatz lösen:

${z(t) = a \,\sin(\omega_0 t)\,\,}$

Wenn man den Ansatz in die Differentialgleichung einsetzt, ergibt sich

$(c - \omega_0^2 m) \sin(\omega_0 t) = 0$

was nur dann für alle Zeiten t gilt, wenn der Koeffizient der Sinusfunktion für sich alleine null ist.

$c - \omega_0^2 m = 0 \Rightarrow \omega_0 = \sqrt{\frac{c}{m}}$

${\omega_0 \,}$ ist die ungedämpfte Eigenkreisfrequenz. Sie ist ${2 \pi\,}$ mal so groß wie die Eigenfrequenz. Das Federpendel schwingt also mit der Periodendauer T = 2π / ω₀.

Wenn man die Feder an ihrem oberen Ende mit dem Weg ${z_0\sin(\omega t)\,}$ zwangsbewegt, entspricht die Federkraft nicht mehr der gesamten Auslenkung der Kugel, sondern nur noch der Differenz zur Auslenkung am gegenüberliegenden Ende der Feder. Die allererste Gleichung geht damit über in

$m \ddot z = - c (z(t) - z_0\sin(\omega t)) \Rightarrow m \ddot z + c z(t) = c z_0 \sin(\omega t)$

Die homogene Lösung entspricht dem oben beschriebenen Problem und stellt eine freie Schwingung in der Eigenfrequenz dar, deren Amplitude und Phasenlage von den Anfangsbedingungen abhängt. Ihr überlagert sich als Partikulärlösung die erzwungene Schwingung

$z(t) = \frac{c/m}{c/m - \omega^2}\,z_0\,\sin(\omega t) = \frac{\omega_0^2}{\omega_0^2 - \omega^2}\,z_0\,\sin(\omega t) = \frac{1}{1 - (\omega/\omega_0)^2}\,z_0\,\sin(\omega t)$

Die Amplituden werden im Resonanzfall ${ \omega = \omega_0\,}$ unendlich groß, wenn die Dämpfung vernachlässigt wird. Mit Dämpfung, die in der Realität immer vorhanden ist, werden die Amplituden nicht mehr unendlich groß, es entsteht aber immer noch ein Peak im Bereich der Eigenfrequenz. Die Eigenfrequenz(en) der meisten Systeme ändern sich infolge Dämpfung nur so geringfügig, dass die ungedämpften Eigenfrequenzen von Interesse bleiben.

Ein Freiheitsgrad bei einer schwingenden Luftsäule oder einer elektrischen Welle

Dem „festen“ Ende einer Welle entspricht das offene Ende einer Luftsäule in einem Rohr, weil dort der Luftdruck konstant ist. Umgekehrt entspricht das „freie“ Ende einer Welle dem druckfesten Abschluss einer schwingenden Luftsäule.

• 

  Schwingungsformen bei einem festen und einem freien Ende

• 

  Schwingungsformen bei zwei festen Enden

• 

  Schwingungsformen bei zwei freien Enden

Mehrere Freiheitsgrade

Systeme mit mehreren Freiheitsgraden werden in Analogie dazu mit einer Matrizengleichung beschrieben:

$[M] \frac{\partial^2 \{X\}}{\partial t^2} +[B] \frac{\partial \{X\}}{\partial t} + [C] \{X\} = \{F\}$.

Darin ist [M] die Massenmatrix, [B] die Dämpfungsmatrix, [C] die Steifigkeitsmatrix und {F} der Lastvektor. Eine Untersuchung der freien Schwingungen des ungedämpften Systems führt zum allgemeinen Eigenwertproblem

${\,([C] - \omega^2 [M])\{X\} = 0 \,}$

Dies kann in ein spezielles Eigenwertproblem umgerechnet werden, wie unter "Eigenwertproblem" beschrieben, um die Eigenfrequenzen des Systems zu berechnen.

Unendliche Freiheitsgrade

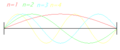
Systeme mit unendlich vielen Freiheitsgraden weisen unendlich viele Eigenfrequenzen auf, beispielsweise ein beidseitig gelenkig gelagerter Biegebalken mit der Biegesteifigkeit EI und der Masse pro Längeneinheit m, dessen Durchbiegung w(x,t) sich abhängig von Ort x und Zeit t aus folgender Differentialgleichung ergibt:

$EI\,\frac{\partial^4 w}{\partial x^4} + m\frac{\partial^2 w}{\partial t^2} = 0$

Die beidseitig gelenkige Lagerung wird durch ein ganzes Vielfaches an Halbwellen erfüllt, und der entsprechende Ansatz

$w(x,t) = \sin\left(\frac{j\pi x}{L}\right) \sin(\omega t)$

ergibt die Eigenfrequenzen

$\omega_j = \sqrt{\frac{EI}{m} \left(\frac{j\pi}{L}\right)^4} \quad;\quad j=1,2,3,\ldots$

Beispiele

• Eine Glocke, die angeschlagen wird, schwingt anschließend mit den Eigenfrequenzen. Durch Dämpfung klingt die Schwingung über die Zeit ab. Dabei werden höhere Frequenzen schneller abgedämpft als tiefere.
• Eine Stimmgabel ist so konstruiert, dass außer der tiefsten Eigenfrequenz (Kammerton a, 440Hz) kaum weitere Eigenschwingungen angeregt werden.
• Auch in Gebäuden können Eigenfrequenzen angeregt werden. Wenn beim Nachbarn Musik durchaus sehr leise läuft, kann es vorkommen, dass die Bässe mit einer Eigenfrequenz des Gebäudes gleichfrequent sind, was sich als lautes Wummern äußert, ohne dass die Musik als solche hörbar wäre.
• Ein Beispiel, welches im Physikunterricht oft gezeigt wird, ist die Tacoma Narrows Bridge, die im Jahre 1940 in Schwingung geriet und nach nur 4 Monaten Betriebszeit einstürzte (Resonanzkatastrophe).
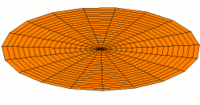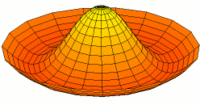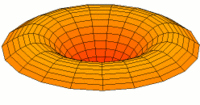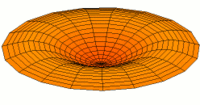
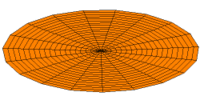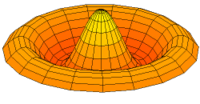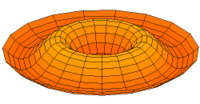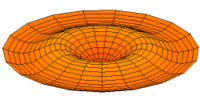
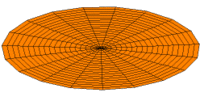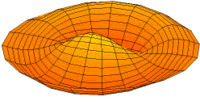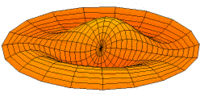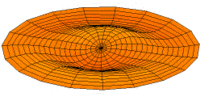
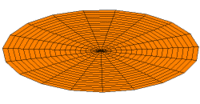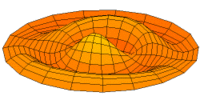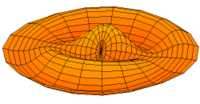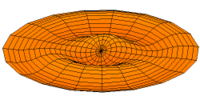
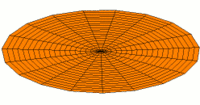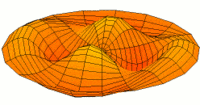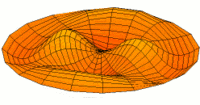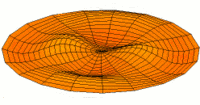
• Trommeln zeigen eine Vielfalt von möglichen Eigenfrequenzen, wie im Bild dargestellt. Da die Membranen von Lautsprechern im Zentrum angetrieben werden, kommen nur die Moden u_0x (obere Bildreihe) in Frage. Die Partialschwingungen führen zu einer unerwünschten Beeinträchtigung der Wiedergabequalität. Die Benennungen sind die der entsprechenden Kugelflächenfunktionen dieser Schwingungen.

• 

  Mode u₀₁ (1s)

• 

  Mode u₀₂ (2s)

• 

  Mode u₀₃ (3s)

• 

  Mode u₁₁ (2p)

• 

  Mode u₁₂ (3p)

• 

  Mode u₁₃ (4p)

• 

  Mode u₂₁ (3d)

• 

  Mode u₂₂ (4d)

• 

  Mode u₂₃ (5d)

Einzelnachweise

1. ↑ Grundlagen der Schwingungstechnik. 2. Systeme mit mehreren Freiheitsgraden, kontinuierliche Systeme, Studium Technik, Band 2 von Grundlagen der Schwingungstechnik, Horst Irretier, ISBN 3528039078, Seite 23 Online

Literatur

• Dieter Meschede: Gerthsen Physik. 23. Auflage, Springer-Verlag, Berlin Heidelberg New York, 2006, ISBN 978-3-540-25421-8
• Hans-Ulrich Harten: Physik für Mediziner. 6. Auflage, Springer-Verlag, Berlin Heidelberg New York, 1993, ISBN 3-540-56759-3

Siehe auch

• Harmonische
• Oberton
• Eigenform
• Vergrößerungsfunktion
• Beckenschwingung

Weblinks

• Eigenschwingungsformen von runden Platten
• Interaktive Simulation von Wellen in einer runden Membran ("Trommel") (Java; englisch)