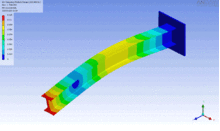
Eigenform

Dieser Artikel wurde den Mitarbeitern der Redaktion Physik zur Qualitätssicherung aufgetragen. Wenn Du Dich mit dem Thema auskennst, bist Du herzlich eingeladen, Dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der Meinungsaustausch darüber findet derzeit nicht auf der Artikeldiskussionsseite, sondern auf der Qualitätssicherungs-Seite der Physik statt.

Die Eigenform, Eigenschwingungsform, Eigenschwingform oder Mode (von engl. mode -s, dort vom lat. modus; Plural: Moden), auch Schwingungsmode und wird in der Akustik überwiegend Raummode genannt. Diese beschreibt vorwiegend stationäre Eigenschaften stehender Wellen mit einer Eigenfrequenz z. B. in einer Pfeife, einem Hohlraumresonator oder auf einer Saite. Bei Hohlleitern, Laserstrahlen oder Glasfaserkabeln, werden damit aber auch fortlaufende Wellen hinsichtlich ihrer Energieverteilung, in verschieden Richtungen beschrieben. Da die Angabe von Moden auch zur Beschreibung fortlaufender Wellen benutzt wird, hebt sich der Begriff von Normalschwingungen ab, die sich nur auf stehende Wellen oder oszillierende Systeme beziehen.

Die Wellen können akustisch (Schall, Körperschall, Schwingquarz) oder elektromagnetisch (Funkwellen, Mikrowellen, Laserstrahl, Licht) sein.

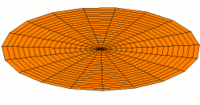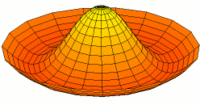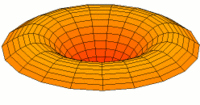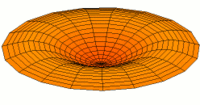
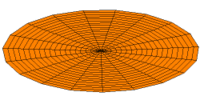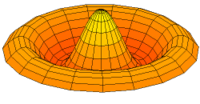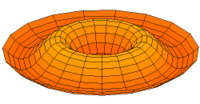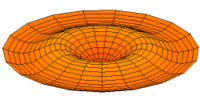
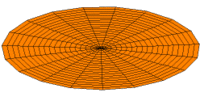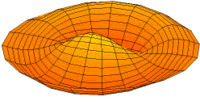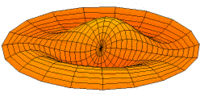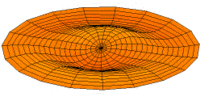
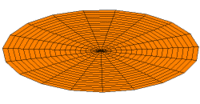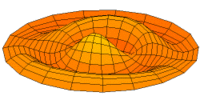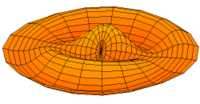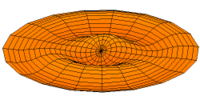
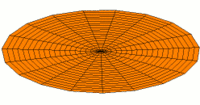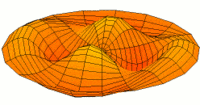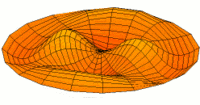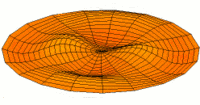
Vibration einer kreisförmigen Scheibe in zwei Dimensionen. Die Scheibe vibriert in einem single mode. Siehe andere Modi.

Die Eigenform ist die geometrische Form, mit der ein Körper während einer Eigenschwingung schwingt und die er bei der größten Auslenkung annimmt. Die Schwingung pendelt dabei zwischen zwei gegensätzlichen Auslenkungszuständen. Die Eigenform zeigt also, wo sie sich Schwingungsknoten Schwingungsbäuche befinden.

Zumindest für den Beobachtungszeitraum wandert die Welle nicht mehr durch die Struktur, sondern hat feste Amplituden Maxima und Minima. Die Schwingungknoten sind Amplituden Nullstellen. Das heißt, an der Stelle, an der ein Knoten auftritt, ist keine Auslenkung zu erkennen.

„Bei [...] erzwungen Schwingungen bilden sich nur die Schwingungsformen aus, deren Charakteristik der der Erregereinwirkung entspricht. In allen angeregten Eigenformen verläuft die Schwingung aber mit der Erregerfrequenz. Werden alle n Eigenfrequenzen erregt, so weist die Resonanzkurve, d. h. der Amplitudengang, bei jeder n Eigenfrequenzen ein Extremum auf. Es treten also so viele Extrema auf, wie das System Freiheitsgrade hat. “

– Heinrich Frohne, Karl-Heinz Löcherer, Hans Müller, Franz Moeller ^[1]

In eindimensionalen Strukturen ist die Anzahl der Knoten um eins niedriger als die Nummer der Eigenfrequenz. Die Form, mit der ein Festkörper schwingt, wird durch die Eigenfunktion und Eigenenwerte beschrieben. Sehr häufig wird in diesen Zusammenhang die Finite-Elemente-Methode für Berechnungen eingesetzt.^[2]

Anregung von Eigenformen

Körper können mit verschiedenen Eigenfrequenzen schwingen und bei jeder Frequenz gibt es eine charakteristische Eigenschwingungsform, die auch kurz „Eigenform“ oder „Mode“ genannt wird. Eigenfrequenzen und dazugehörige Moden eines Körpers sind abhängig von dessen Lagerung bzw. Einspannung und den physikalischen Eigenschaften und Abmessungen. Der einfachste Fall ist vereinfacht bei den meisten Musikinstrumenten gegeben, bei denen bevorzugt nur eine eindimensionale Schwingung mit Harmonischen vorkommt. Bei Membranen, Platten, Stäben und Hohlräumen, gibt es sechs Freiheitsgrade was zu einer mehrdimensionalen Zusammensetzung der möglichen Frequenzen und deren Schwingungsformen führt. Grundsätzlich wird die Anzahl der maximal möglichen Freiheitsgrade durch die Zwangsbedingungn wieder reduziert. Einseitig eingespannte Schwinger weichen bereits beim ersten Freiheitsgrad stark von dem ganzzahligen Vielfachen bei Harmonischen ab. Im Falle einer Saite oder Stimmgabel macht sich das durch Schallabstrahlung in hörbaren Tönen bemerkbar. Die erste Eigenschwingung erzeugt den Grundton, die höheren Eigenschwingungen werden auch als Obertöne bezeichnet. Eigenschwingungen treten praktisch niemals isoliert auf. Stattdessen schwingt ein Körper in allen seinen Moden gleichzeitig, die aber unterschiedlich stark angeregt sind. Bei einer Saite wird üblicherweise der Grundton am stärksten angeregt und weitere Eigenschwingungen haben einen geringeren Anteil. Durch spezielle Anschlagtechniken oder Spieltechniken lassen sich aber auch höhere Eigenschwingungen bevorzugt anregen.

Gleichungen

„Durch geeignete Wahl der Anregungswerte $\textstyle y_0, \dot{y_0}$ lassen sich „reine“ Eigenschwingungen erzeugen. In diesen Fall bewegt sich jeder Teilkörper mit der selben Eigenfrequenz $\textstyle \omega_j$ [...], alle anderen Eigenschwingungen werden unterdrückt. [...] Man bezeichnet ein Tipel {$\textstyle {\omega_j, v_j}$} mit der Lösung

$y_j(t) \ = \ v_j \ (a_j \ cos \ \omega_j \ t \ + \ b_j \ sin \ \omega_j \ t), \ \omega_j \ = \ \sqrt{\lambda_j}$

als Eigenform [...] [des konservativen Mehrkörpersystems], da der Eigenvektor $\textstyle {v_j}$ aufgrund der freien Skalierung bloß die Form der Eigenschwingung festlegt (engl. mode shape) und nicht die tatsächliche Amplitude. [...]

Allgemeine Lösung

Die allgemeine Lösung ergibt sich durch eine lineare Überlagerung der $\textstyle N_{FG}$ Eigenformen. Für den Fall von unterschiedlichen Eigenwerten $\textstyle \lambda_j$ erhält man

$y_j(t) \ = \ \sum^{N_{FG}}_{j=1} \ v_j \ (a_j \ cos \ \omega_j \ t \ + \ b_j \ sin \ \omega_j \ t), \ \omega_j \ = \ \sqrt{\lambda_j}$

Die $\textstyle 2N_{FG}$ freien Parameter $\textstyle a_j, b_j$ bestimmen die Phasenlage der Einschwingungen, sie sind durch die $\textstyle 2N_{FG}$ vorgegebenen Parameter $\textstyle y_0, \dot{y_0}$ ungedämpfte Schwingung $\textstyle y$ eindeutig bestimmt. Jede Lagerkoordinate $\textstyle y_j(t), i=1,...,N_{FG}$ enthält also überlagerte Schwingungsanteile aller Eigenfrequenzen mit den relativen Schwingungsamplituden $\textstyle v_{j,i}$.^[3] “ (Klaus Janschek)

Ordnungszahl

Die Frequenzen und Eigenschwingungsformen werden nach ihrer Ordnungszahl (Nummer) benannt, also:

1. Die erste Eigenschwingungsform oder Grundform stellt sich bei einer Schwingung mit der ersten Eigenfrequenz, bei der Grundfrequenz ein.
2. Die zweite Eigenschwingungsform schwingt mit der zweiten Eigenfrequenz.
3. usw.
   

Ist die Zusammensetzung der Eigenfrequenzen komplexer wie bei Räumen, so wird die Ordnungszahl mehrstellig oder durch Komma getrennt in Klammern angegeben.

Praktisches Beispiel

Die erste Eigenform eines Lineals erhält man, wenn man ein Ende auf einen Tisch legt und festhält und auf das andere Ende drückt und loslässt. Das Lineal schwingt sichtbar in seiner ersten Eigenfrequenz für diese Anordnung.

Hohlraummoden in der Akustik

Der einseitig geschlossene Hohlraumresonator unter der Stimmgabel ist abgestimmt auf 1/4 der Wellenlänge (19 cm bei 440 Hz) und verstärkt die Lautstärke erheblich.

Helmholtz-Resonator aus Messing von ca. 1900

Akustische Hohlraumresonatoren sind z. B. der Helmholtz-Resonator oder das Kundtsche Rohr, sie spielen aber auch bei Lautsprecherboxen (Bassreflexbox) und bei Blasinstrumenten und Orgelpfeifen eine große Rolle. Beim Helmholtz-Resonator und bei Bassreflexboxen unterliegen die Grundresonanzen anderen Gesetzen; hier schwingt die Luftmasse im Hals bzw. im Bassreflexrohr gegen die Elastizität des Volumens, die Grundresonanzen sind niedriger als es die geometrischen Abmessungen erwarten lassen.

In der Akustik spielen beidseitig und einseitig offene sowie geschlossene Hohlraumresonatoren eine große Rolle. Beidseitig offene Rohre besitzen ihre Grundresonanz bei der halben Schallwellenlänge.

Einseitig offene Rohre besitzen ihre Grundresonanz bei einem Viertel der Schallwellenlänge:

• gedackte Orgelpfeifen, Posaunen, Trompeten; hier sind ungeradzahlige Oberwellen bzw. geradzahlige Harmonische anregbar.

Eine stehende Welle. Wie man hier erkennen kann, erscheint an den Enden (der Raumbegrenzung) jeweils als Maximum ein Druckbauch.

Geschlossene Resonatoren

→ Hauptartikel: Raummode

Während kleine Räume ausgesprochen diskrete Eigenfrequenzen aufweisen, überlagern sich bei großen Räumen (z.B. Kirchen) alle Moden zu einem Kontinuum – es tritt Hall auf.

Eine bestimmte Resonanzfrequenzverteilung ist eine physikalische Eigenschaft des Raumes, die von seinen Abmessungen abhängig ist. Nur bestimmte Frequenzen werden angeregt. Bei diesen Resonanzeffekten spielt sowohl der erhöhte Pegel als auch die zeitliche Fortdauer des Tons eine Rolle.

Licht und Laser Moden

In einem Laser, wird Licht einer bestimmten Frequenz in einem Hohlraumresonator verstärkt, der gewöhnlich aus einer Anordnung aus zwei oder – bei gefaltetem Resonator – aus mehreren Spiegeln besteht. Hier wie auch beim Fabry-Pérot-Interferometer läuft das Licht nur in einer Richtung zwischen den Spiegeln hin- und her. Die Eigenresonanzen heißen beim Laser Longitudinalmoden. Liegen mehrere dieser Moden innerhalb des Verstärkungsbereiches des aktiven Mediums des Lasers, kann dieser zugleich oder wahlweise auf einer dieser diskreten Moden bzw. Frequenzen arbeiten. Bei der Modenkopplung (mode locking) sind mehrerer dieser Moden synchronisiert und überlagern sich zu einem hin- und herlaufenden Impuls.

Elektromagnetische Moden

→ Hauptartikel: Transversalelektromagnetische Welle

Bei elektromagnetischen Wellen wie Licht, Laser und Funkwellen werden die folgenden Typen von Moden unterschieden:

• TEM- oder Transversal-Elektromagnetische Mode: Sowohl die elektrische, als auch die magnetische Feldkomponente stehen stets senkrecht zur Ausbreitungsrichtung. Diese Mode ist nur ausbreitungsfähig, wenn entweder
  • zwei voneinander isolierte Leiter (Äquipotentialflächen) zur Verfügung stehen, beispielsweise in einem Koaxialkabel oder
  • kein elektrischer Leiter vorhanden ist, beispielsweise in Gas-Lasern oder Lichtwellenleitern.
• TE- oder H-Moden: Nur die elektrische Feldkomponente steht senkrecht zur Ausbreitungsrichtung, während die magnetische Feldkomponente in Ausbreitungsrichtung zeigt.
• TM- oder E-Moden: Nur die magnetische Feldkomponente steht senkrecht zur Ausbreitungsrichtung, während die elektrische Feldkomponente in Ausbreitungsrichtung zeigt.

Die letzten beiden Modentypen haben besonders in Hohlleitern Bedeutung.

TEM-Wellen sind in ihrer Frequenz nicht beschränkt, das heißt sie sind über das gesamte Frequenzspektrum ausbreitungsfähig. TM- und TE-Wellen hingegen sind nur ab einer bestimmten, von der Geometrie des Leiters abhängigen Frequenz (cut-off-Frequenz) ausbreitungsfähig. Folglich können bei einer festen Frequenz auch mehrere Moden gleichzeitig ausbreitungsfähig sein. In der Datenübertragung ist dieser Zustand jedoch unerwünscht, da Signalintegrität, das heißt dispersionsarmer Betrieb von Wellenleitern, nur bei Modenreinheit gewährleistet werden kann. Wellenleiter (also z. B. Kabel oder Hohlleiter) können also nur bis zur cut-off-Frequenz der ersten höheren Mode sinnvoll zur Signalübertragung verwendet werden.

Oberflächenmoden

Wasser

Bei Wasserwellen und anderen Oberflächenwellen (Schwerewellen bzw. Rayleigh-Wellen) kann in ähnlicher Weise von einem zweidimensionalen Resonator gesprochen werden, wenn die Flächen reflektierend begrenzt sind. Für Tideresonanz stellt die in einer Bucht schwingfähige Wassermasse einen sogenannten Beckenresonator dar; siehe auch Beckenschwingung, Seiche. Bei Wellenresonanzen können vom erregenden Wellenspektrum gleichzeitig mehrere Eigenfrequenzen einer zwischen der Küste und vorgelagerten Riffen schwingfähigen Wassermasse getroffen werden, sodass dieselbe Wassermasse unterschiedliche Beckenresonanzen ausführt.

Festkörper

Verschiedene akustische Schwingungsmoden in Festkörpern treten beispielsweise in Schwingquarzen, Oberflächenwellenfiltern, keramische Resonatoren, in Glocken, Gongs, Klangstäben, Triangeln usw. auf. Alle diese Körper können neben der Grundresonanzfrequenz auch in höheren Schwingungsmoden angeregt werden bzw. weisen aufgrund der unterschiedlichen Zusammensetzung ihrer Schwindungsmoden einen bestimmten Klangcharakter auf. In Festkörpern können aufgrund des vorhandenen Schubmoduls auch transversale Wellen- und Schwingungsmoden auftreten.

Die Form von Gehäusen und Maschinenteilen bestimmt, welche Schwingungsmoden im Betrieb besonders angeregt werden. Durch geeignete, eher unregelmäßige Formgebung kann die Ausbildung von Schwingungsmoden, die auf Formsymmetrien beruhen, vermieden werden. Schallabstrahlung und Ermüdung durch Schwingungen kann so reduziert werden. Bei in Rotation befindlichen mechanischen Teilen spielt das Auswuchten eine besondere Rolle. „Aus der Unwuchtverteilung und der jeweiligen Biegelinie kann die modale Unwucht für jede Eigenform ausgerechnet werden. Sie ist die Summe der Produkte aus einer einzelnen Unwucht und dem Biegefeld der Eigenform in dieser Ebene. “ (Hatto Schneider ^[4]).

Sicherheit von Bauwerken

Eigenformen spielen auch bei der Überfahrsimulation von Brücken bei der Bahn eine besondere Rolle. „Zur Überfahrsimulation wird der InterRegio mit einer elektrischen Lok BR103 und / Riesenwagen herangezogen. Die Lok und die Riesenwagen werden wieder als strukturdiskrete Mehrkörpersysteme abgebildet.“ (Marc Weiner. ^[5])

Membrane

Eine eingespannte Fläche wie bei einer Trommel zeigt sehr viele unterschiedliche Schwingungsmoden. Diese Partialschwingungen führen bei Lautsprechern zu Unregelmäßigkeiten im Frequenzgang. „Die 1. Eigenform einer kreisförmigen Membran ist die sogenannte 01-Mode (Eigneform englisch: Mode). [...] stellt diese Eigenform den Grundton dar. “ (Hatto Schneider ^[4])

• 

  Mode u₀₁ (1s)

• 

  Mode u₀₂ (2s)

• 

  Mode u₀₃ (3s)

• 

  Mode u₁₁ (2p)

• 

  Mode u₁₂ (3p)

• 

  Mode u₁₃ (4p)

• 

  Mode u₂₁ (3d)

• 

  Mode u₂₂ (4d)

• 

  Mode u₂₃ (5d)

Biegeschwinger

Der einseitig eingespannte Biegeschwinger dargestellt ist nur die erste Eigenfrequenz

Einseitig eingespannte Stäbe nennt man Biegeschwinger; Auch diese können auf mehreren Eigenfrequenzen schwingen.

Einzelnachweise

1. ↑ Moeller Grundlagen der Elektrotechnik, Heinrich Frohne, Karl-Heinz Löcherer, Hans Müller, Franz Moeller, 2005, ISBN 3519664003, Seite 349 Online
2. ↑ „Zur Kontrolle, ob mit der Vektoriteration tatsächlich der gewünschte Eigenwert und seine Eigenform berechnet wurde, wird erneut das Matritzenzerlegungsverfahren herangezogen.“ Matthias Kraus Finite-Elemente-Methoden im Stahlbau, Rolf Kindmann, Matthias Kraus, 2007, ISBN 3433018375, Seite 65,66, 366 Online
3. ↑ Systementwurf Mechatronischer Systeme: Methoden Modelle Konzepte, Klaus Janschek, 2009, ISBN 3-540-78876-X, Seite 248, 249 Online
4. ↑ ^{a b} Auswuchttechnik (VDI-Buch) Chemische Technik Verfahrenstechnik, Hatto Schneider, 2007, ISBN 3540490914, Seite 56, Online
5. ↑ Beurteilung von verkehrsinduzierten Schwingungen auf Eisenbahnbrücken aus Stahl, Marc Weiner, ISBN 3638709728, Seite 68,69 Online

Literatur

• Schwingungen Mechanischer Antriebssysteme: Modellbildung, Berechnung, Analyse, Synthese, Hans Dresig, 2005, ISBN 3540260242 Online

• Windkraftanlagen: Grundlagen, Entwurf, Planung und Betrieb, R. Gasch, 2009, ISBN 3834806935, Seite 306 Online

• Erdbebensicherung von Bauwerken, Hugo Bachmann, 2002, ISBN 3764369418, Seite 181 Online

Siehe auch

• Transversalelektromagnetische Welle
• Eigenfrequenz
• Normalschwingung
• Shuntimpedanz

Weblinks

• Graphische Beispiele von Moden einer zwischen zwei Punkten eingespannen Saite
• Berechnung der drei Raummoden von Rechteck-Räumen (Stehende-Wellen-Berechnung)
• Java-Applet zur Visualisierung akustischer Moden in beliebigen rechteckigen Räumen
• Der Unterschied zwischen den Moden als Schalldruckverteilung in Räumen und den Moden der Saitenschwingungen
• Eigenschwingungsformen von runden Platten