Moden

Dieser Artikel wurde den Mitarbeitern der Redaktion Physik zur Qualitätssicherung aufgetragen. Wenn Du Dich mit dem Thema auskennst, bist Du herzlich eingeladen, Dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der Meinungsaustausch darüber findet derzeit nicht auf der Artikeldiskussionsseite, sondern auf der Qualitätssicherungs-Seite der Physik statt.

Die ersten sechs Eigenschwingungen (Moden) eines Resonators mit parallelen Wänden. Anmerkung: An den Wänden sollte dabei maximaler Schalldruck herrschen, also Druckbäuche und keine Knoten zu finden sein. Die Darstellung zeigt eine schwingende Saite mit ihren Schwingungsmoden.

Als Moden (von engl. mode -s, dort vom lat. modus), auch Schwingungsmoden, in der Akustik überwiegend Raummoden genannt, bezeichnet man in der Physik die stationären Eigenschaften stehender Wellen (z. B. in einer Pfeife, einem Hohlraumresonator oder auf einer Saite) und auch fortlaufender Wellen (z. B. in einem Hohlleiter, Laserstrahl oder Glasfaserkabel) hinsichtlich ihrer Energieverteilung, in verschieden Richtungen.

Da die Angabe von Moden auch zur Beschreibung fortlaufender Wellen benutzt wird, hebt sich der Begriff von Normalschwingungen ab, die sich nur auf stehende Wellen oder oszillierende Systeme beziehen.

Die Wellen können akustisch (Schall, Körperschall, Schwingquarz) oder elektromagnetisch (Funkwellen, Mikrowellen, Laserstrahl, Licht) sein.

Raummoden in der Akustik

Durch die Raummoden wird der Klang eines Raums verfärbt, weil bestimmte Töne besonders hervortreten und eine ungleichförmige Energieverteilung innerhalb des Raums haben. Treten diskrete Resonanzfrequenzen auf, so sind diese auffälliger, als wenn mehrere Resonanzen gleichmäßig im Spektrum verteilt sind (Nachhall).

Eine stehende Welle. Wie man hier erkennen kann, erscheint an den Enden (der Raumbegrenzung) jeweils als Maximum ein Druckbauch.

Eine bestimmte Resonanzfrequenzverteilung ist eine physikalische Eigenschaft des Raumes, die von seinen Abmessungen abhängig ist. Nur bestimmte Frequenzen werden angeregt. Bei diesen Resonanzeffekten spielt sowohl der erhöhte Pegel als auch die zeitliche Fortdauer des Tons eine Rolle.

Raummoden zwischen zwei harten Wänden. An den Wänden muss dabei immer maximaler Schalldruck herrschen, was dort an den Druckbäuchen zu erkennen ist.

Oberhalb etwa 300 Hz (Schröderfrequenz) verursachen akustische Moden des Raums in Wohnräumen keine hörbaren Verzerrungen der Wiedergabe, weil die Moden in Form von dichten Reflexionen und Nachhall ineinander übergehen. Unterhalb von 300 Hz können sie dagegen eine wahrnehmbare Klangverfärbungen bewirken. Da diese die besonders tiefen Töne betreffen, wird dies als Dröhnen, Booming, oder Ein-Noten-Bass empfunden. Die Amplitude einer akustischen Mode hängt von der Position im Raum ab. Der Grad der Verfärbung ist daher von Ort zu Ort verschieden.

Es gibt in der Akustik drei Arten stehender Moden, die in einem typischen (quaderförmigen) Hörraum vorkommen. Dieses sind axiale (longitudinale), tangentiale und diagonale Moden (auch Obligue- oder Schrägmoden genannt). Weil die axialen Moden deutlich dominieren, sind diese besonders wichtig.

Um für einen Rechteckraum axiale, oblique und tangentiale Moden in ihrer Frequenz zu berechnen, wird folgende Formel verwendet:

$f = \frac{c_S}{2} \sqrt{\left(\frac{n_x}{L}\right)^2 + \left(\frac{n_y}{B}\right)^2 + \left(\frac{n_z}{H}\right)^2} \,$

Hierbei ist:

• f die Frequenz der Mode in Hz
• c_S die Schallgeschwindigkeit 343 m/s
• n_x die Ordnung der Mode Raumlänge
• n_y die Ordnung der Mode Raumbreite
• n_z die Ordnung der Mode Raumhöhe
• L, B, H sind Länge, Breite und Höhe des Raums in Meter

Weitere akustische Schwingungsmoden

Der einseitig eingespannte Biegeschwinger - Dargestellt ist nur die erste Mode

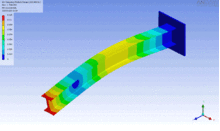
Biegeschwinger

Einseitig eingespannte Stäbe nennt man Biegeschwinger; Auch diese können in mehreren Moden schwingen.

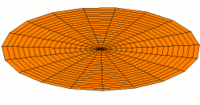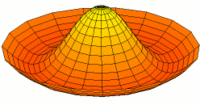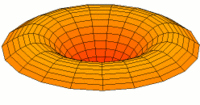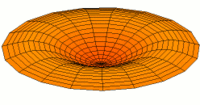
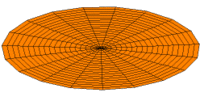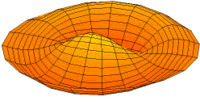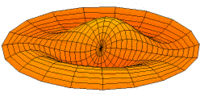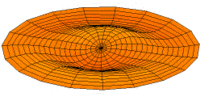
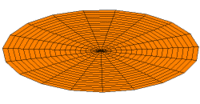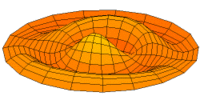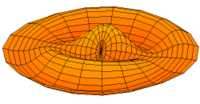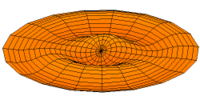
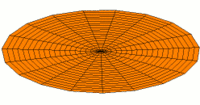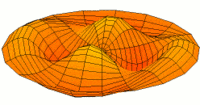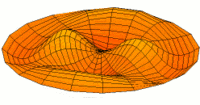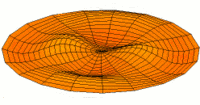
Membrane

Eine eingespannte Fläche wie bei einer Trommel zeigt sehr viele unterschiedliche Schwingungsmoden. Diese Partialschwingungen führen bei Lautsprechern zu Unregelmäßigkeiten im Frequenzgang.

• 

  Mode u₀₁ (1s)

• 

  Mode u₀₂ (2s)

• 

  Mode u₀₃ (3s)

• 

  Mode u₁₁ (2p)

• 

  Mode u₁₂ (3p)

• 

  Mode u₁₃ (4p)

• 

  Mode u₂₁ (3d)

• 

  Mode u₂₂ (4d)

• 

  Mode u₂₃ (5d)

Hohlräume

Akustische Hohlraumresonatoren sind z. B. der Helmholtz-Resonator oder das Kundtsche Rohr, sie spielen aber auch bei Lautsprecherboxen (Bassreflexbox) und bei Blasinstrumenten und Orgelpfeifen eine große Rolle.

Festkörper

Verschiedene akustische Schwingungsmoden in Festkörpern treten beispielsweise in Schwingquarzen, in Glocken, Gongs, Klangstäben, Triangeln usw. auf. Alle diese Körper können neben der Grundresonanzfrequenz auch in höheren Schwingungsmoden angeregt werden bzw. weisen aufgrund der unterschiedlichen Zusammensetzung ihrer Schwindungsmoden einen bestimmten Klangcharakter auf. In Festkörpern können aufgrund des vorhandenen Schubmoduls auch transversale Wellen- und Schwingungsmoden auftreten.

Dis Form von Gehäusen und Maschinenteilen bestimmt, welche Schwingungsmoden im Betrieb besonders angeregt werden. Durch geeignete, eher unregelmässsige Formgebung kann die Ausbildung von Schwingungsmoden, die auf Formsymmetrien beruhen, vermieden werden. Schallabstrahlung und Ermüdung durch Schwingungen kann so reduziert werden.

Elektromagnetische Wellen

Bei Elektromagnetische Wellen, wie Licht, Laser und Funkwellen, werden die folgenden Typen von Moden unterschieden:

• TEM- oder Transversal-Elektromagnetische Mode: Sowohl die elektrische, als auch die magnetische Feldkomponente stehen stets senkrecht zur Ausbreitungsrichtung. Diese Mode ist nur ausbreitungsfähig, wenn entweder
  • zwei voneinander isolierte Leiter (Äquipotentialflächen) zur Verfügung stehen, beispielsweise in einem Koaxialkabel oder
  • kein elektrischer Leiter vorhanden ist, beispielsweise in Gas-Lasern oder Lichtwellenleitern.
• TE- oder H-Moden: Nur die elektrische Feldkomponente steht senkrecht zur Ausbreitungsrichtung, während die magnetische Feldkomponente in Ausbreitungsrichtung zeigt.
• TM- oder E-Moden: Nur die magnetische Feldkomponente steht senkrecht zur Ausbreitungsrichtung, während die elektrische Feldkomponente in Ausbreitungsrichtung zeigt.

Die letzten beiden Modentypen haben besonders in Hohlleitern Bedeutung.

TEM-Wellen sind in ihrer Frequenz nicht beschränkt, das heißt sie sind über das gesamte Frequenzspektrum ausbreitungsfähig. TM- und TE-Wellen hingegen sind nur ab einer bestimmten, von der Geometrie des Leiters abhängigen Frequenz (cut-off-Frequenz) ausbreitungsfähig. Folglich können bei einer festen Frequenz auch mehrere Moden gleichzeitig ausbreitungsfähig sein. In der Datenübertragung ist dieser Zustand jedoch unerwünscht, da Signalintegrität, das heißt dispersionsarmer Betrieb von Wellenleitern, nur bei Modenreinheit gewährleistet werden kann. Wellenleiter (also z. B. Kabel oder Hohlleiter) können also nur bis zur cut-off-Frequenz der ersten höheren Mode sinnvoll zur Signalübertragung verwendet werden.

Siehe auch

• Transversalelektromagnetische Welle
• Eigenfrequenz

Weblinks

• Graphische Beispiele von Moden einer zwischen zwei Punkten eingespannen Saite
• Der Unterschied zwischen den Moden als Schalldruckverteilung in Räumen und den Moden der Saitenschwingungen
• Berechnung der drei Raummoden von Rechteck-Räumen (Stehende-Wellen-Berechnung)
• Java-Applet zur Visualisierung akustischer Moden in beliebigen rechteckigen Räumen