Kugelflächenfunktionen

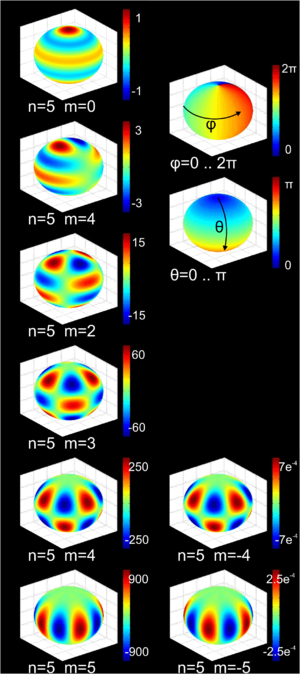
Veranschaulichung einiger Kugelflächenfunktionen (um die z-Achse rotierend). Dargestellt ist Y_l,m, wobei l der Zeile und m der Spalte entspricht. Zeilen und Spalten werden jeweils bei null beginnend durchnummeriert.

Die Kugelflächenfunktionen sind ein vollständiger und orthonormaler Satz von Eigenfunktionen des Winkelanteils des Laplace-Operators. Dieser Winkelanteil zeigt sich, wenn der Laplace-Operator in Kugelkoordinaten geschrieben wird. Die Eigenwertgleichung lautet:

$\left(\frac{\partial^{2}}{\partial\vartheta^{2}}+\frac{\cos\vartheta}{\sin\vartheta}\frac{\partial}{\partial\vartheta}+\frac{1}{\sin^{2}\vartheta}\frac{\partial^{2}}{\partial\varphi^{2}}\right)Y_{lm}(\vartheta,\varphi)=-l(l+1)Y_{lm}(\vartheta,\varphi)$

Die Eigenfunktionen sind die Kugelflächenfunktionen, dabei sind N_lm Normierungsfaktoren und P_lm(z) die zugeordneten Legendrepolynome (Details siehe unten):

$Y_{lm}:\;\left[0,\pi\right]\times\left[0,2\pi\right]\rightarrow\mathbb{C},\quad(\vartheta,\varphi)\mapsto\frac{1}{\sqrt{2\pi}}\, N_{lm}\, P_{lm}(\cos\vartheta)\, e^{im\varphi}$ $\quad \text{mit}\quad N_{lm} := \sqrt{\tfrac{2l+1}{2}\,\tfrac{(l-m)!}{(l+m)!}}$

Besonders in der theoretischen Physik haben die Kugelflächenfunktionen eine große Bedeutung für die Lösung partieller Differentialgleichungen. Sie treten zum Beispiel bei der Berechnung von Atomorbitalen auf, da die beschreibende zeitunabhängige Schrödingergleichung den Laplace-Operator enthält und sich das Problem am besten in Kugelkoordinaten lösen lässt. Auch die in der Elektrostatik auftretenden Randwertprobleme können elegant durch die Entwicklung nach Kugelflächenfunktionen gelöst werden. In der Geophysik und Geodäsie werden die Kugelflächenfunktionen bei der Approximation des Geoids und des Magnetfeldes verwendet.

Zusammenhang mit dem Laplace-Operator

Der Winkelanteil des Laplace-Operators zeigt sich, wenn dieser in Kugelkoordinaten geschrieben wird:

$\Delta=\frac{\partial^{2}}{\partial r^{2}}+\frac{2}{r}\frac{\partial}{\partial r}+\frac{1}{r^{2}}\left(\frac{\partial^{2}}{\partial\vartheta^{2}}+\frac{\cos\vartheta}{\sin\vartheta}\frac{\partial}{\partial\vartheta}+\frac{1}{\sin^{2}\vartheta}\frac{\partial^{2}}{\partial\varphi^{2}}\right)=\Delta_{r}+\frac{1}{r^{2}}\Delta_{\vartheta,\varphi}$

Der rechte, eingeklammerte Teil wird hier als Winkelanteil $\Delta_{\vartheta,\varphi}$ bezeichnet. Er ist direkt proportional zum Quadrat des Drehimpulsoperators $\hat{\mathbf{L}}^2=-\hbar^{2} \Delta_{\vartheta,\varphi}$.

Die Laplacesche Differentialgleichung in Kugelkoordinaten

$\Delta f(r,\vartheta,\varphi)\ = 0$

hat neben der trivialen Lösung, f = 0, verschiedenste Lösungen mit vielen technischen Anwendungen.

Zur Lösung wird folgender Produktansatz verwendet, wobei R_l(r) nur vom Radius und $Y_{lm}(\vartheta,\varphi)$ nur von Polar- und Azimutwinkel abhängt:

$f(r,\vartheta,\varphi) = R_{l}(r) Y_{lm}(\vartheta,\varphi)$

Ergibt eingesetzt:

$\Delta R_{l}(r)Y_{lm}(\vartheta,\varphi)=Y_{lm}(\vartheta,\varphi)\Delta_{r}R_{l}(r)+\frac{R_{l}(r)}{r^{2}}\Delta_{\vartheta,\varphi}Y_{lm}(\vartheta,\varphi)=0$

Multiplikation von r² und Division durch $R_{l}(r) Y_{lm}(\vartheta,\varphi)$ liefert:

$\frac{r^{2}\Delta_{r}R_{l}(r)}{R_{l}(r)}+\frac{\Delta_{\vartheta,\varphi}Y_{lm}(\vartheta,\varphi)}{Y_{lm}(\vartheta,\varphi)}=0$

Diese Gleichung kann nur erfüllt werden, wenn in beiden Summanden unabhängig voneinander Radius und Winkel variierbar sind. Beide Summanden müssen somit denselben konstanten Wert annehmen, der zu l(l + 1) gewählt wird (diese Festlegung erweist sich später als sinnvoll):

$\frac{r^{2}\Delta_{r}R_{l}(r)}{R_{l}(r)}=l(l+1)=-\frac{\Delta_{\vartheta,\varphi}Y_{lm}(\vartheta,\varphi)}{Y_{lm}(\vartheta,\varphi)}$

Durch dieses Verfahren, welches Separationsansatz genannt wird, wurde also das ursprüngliche Problem, nämlich die Lösung der Laplace-Gleichung (partielle Differentialgleichung mit drei unabhängigen Variablen), auf das einfachere Problem der Lösung einer gewöhnlichen Differentialgleichung (Radialgleichung)

$\Delta_{r}R_{l}(r)=\frac{l(l+1)}{r^{2}}R_{l}(r)$

und einer partiellen Differentialgleichung mit zwei unabhängigen Variablen (winkelabhängige Gleichung) reduziert.

$\Delta_{\vartheta,\varphi}Y_{lm}(\vartheta,\varphi)=-l(l+1)Y_{lm}(\vartheta,\varphi)$

Nun lässt sich aufgrund der Orthogonalität und Vollständigkeit der Kugelflächenfunktionen zeigen, dass sich jede quadratintegrable Funktion aus diesen speziellen Funktionen als Summe zusammensetzen lässt:

$f(r,\vartheta,\varphi)\ = \sum_{lm}R_{l}(r)Y_{lm}(\vartheta,\varphi)$

Aufgrund der Linearität des Laplace-Operators lassen sich also durch Addition der Lösungen der Radialgleichung, multipliziert mit den Kugelflächenfunktionen, beliebig viele Lösungen der Laplace-Gleichung konstruieren. Damit ergibt sich automatisch eine Darstellung des Lösungsraumes der Laplace-Gleichung.

Die Kugelfunktionen wurden besonders von Legendre (Kugelfunktionen erster Art), Laplace (Kugelfunktionen zweiter Art) und Carl Gottfried Neumann (Kugelfunktionen mit mehreren Veränderlichen) behandelt.

Lösung der Eigenwertgleichung

Die Eigenwertgleichung

$\left(\frac{\partial^{2}}{\partial\vartheta^{2}}+\frac{\cos\vartheta}{\sin\vartheta}\frac{\partial}{\partial\vartheta}+\frac{1}{\sin^{2}\vartheta}\frac{\partial^{2}}{\partial\varphi^{2}}\right)Y_{lm}(\vartheta,\varphi)=-l(l+1)Y_{lm}(\vartheta,\varphi)$

wird mit folgendem Produktansatz separiert:

$Y_{lm}(\vartheta,\varphi)=\Theta_{lm}(\vartheta)\Phi_{m}(\varphi)$

Umsortieren liefert:

$\underbrace{\frac{\sin^{2}\vartheta}{\Theta_{lm}(\vartheta)}\left(\frac{\partial^{2}}{\partial\vartheta^{2}}+\frac{\cos\vartheta}{\sin\vartheta}\frac{\partial}{\partial\vartheta}\right)\Theta_{lm}(\vartheta)+\sin^{2}(\vartheta)(l(l+1))}_{m^{2}}=\underbrace{-\frac{1}{\Phi_{m}(\varphi)}\frac{\partial^{2}}{\partial\varphi^{2}}\Phi_{m}(\varphi)}_{m^{2}}$

Um beide Seite getrennt voneinander variieren zu können, müssen beide Seiten den gleichen konstanten Wert annehmen. Diese Separationskonstante wird als m² gewählt. Es ergeben sich zwei gewöhnliche Differentialgleichungen, die Polargleichung

$\frac{1}{\Theta_{lm}(\vartheta)}\left(\frac{\partial^{2}}{\partial\vartheta^{2}}+\frac{\cos\vartheta}{\sin\vartheta}\frac{\partial}{\partial\vartheta}\right)\Theta_{lm}(\vartheta)=\frac{m^{2}}{\sin^{2}\vartheta}-l(l+1)$

und die Azimutalgleichung.

$\frac{\partial^{2}}{\partial\varphi^{2}}\Phi_{m}(\varphi)=-m^{2}\Phi_{m}(\varphi)$

Die Azimutalgleichung wird durch Φ_m(φ) = Aexp(imφ) gelöst, wobei die m wegen der Zusatzbedingung der Eindeutigkeit auf der Kugeloberfläche Φ_m(φ + 2π) = Φ_m(φ) eingeschränkt sind auf ganze Zahlen exp(im2π) = 1. Mit $\int_{0}^{2\pi}|\Phi_{m}(\varphi)|^{2}\mathrm{d}\varphi=1$ erhält man die normierte Lösung der Azimutalgleichung:

$\Phi_{m}(\varphi)=\frac{1}{\sqrt{2\pi}}\exp(im\varphi),\quad m\in\mathbb{Z}$

Die Polargleichung kann mit einem Potenzreihenansatz gelöst werden. Die Lösungen sind nur dann endlich, eindeutig und stetig, wenn

$l\in\mathbb{N}_{0},\quad|m|\leq l$.

Dann sind die Lösungen die zugeordneten Legendrepolynome $P_{lm}(\cos\vartheta)$ und mit $\int_{0}^{\pi}|\Theta_{lm}(\vartheta)|^{2}\sin(\vartheta)\mathrm{d}\vartheta=1$ erhält man die normierte Lösung der Polargleichung:

$\Theta_{lm}(\vartheta)= \sqrt{\frac{2l+1}{2}\cdot\frac{(l-m)!}{(l+m)!}}\,\, P_{lm}(\cos\vartheta)$

Die Gesamtlösung des Winkelanteils ist das Produkt aus den beiden erhaltenen Lösungen, nämlich die Kugelflächenfunktionen.

$Y_{lm}(\vartheta,\varphi)=\Theta_{lm}(\vartheta)\Phi_{m}(\varphi)= \frac{1}{\sqrt{2\pi}} \sqrt{\frac{2l+1}{2}\cdot\frac{(l-m)!}{(l+m)!}}\,\, P_{lm}(\cos\vartheta) \exp(im\varphi)$

Darstellung

3D Plot der Kugelflächenfunktionen (hier n statt l und θ statt $\vartheta$) $Y_{nm}(\theta,\varphi)\propto P_{nm}(\cos\theta)\exp(i m \varphi)$ für Grad n = 5

Die Darstellung der Kugelflächenfunktionen $Y_{lm}: S^2\rightarrow \mathbb C$ ergibt sich als Lösung der oben genannten Eigenwertgleichung. Die konkrete Rechnung liefert:

$Y_{lm}(\vartheta,\varphi) := \frac{1}{\sqrt{2\pi}}N_{lm} P_{lm}(\cos \vartheta)e^{im \varphi}$

Dabei sind

$P_{lm} (x):=\frac{(-1)^m}{2^ll!}(1-x^2)^{\frac m2} \frac{d^{l+m}}{dx^{l+m}}(x^2-1)^l$

die zugeordneten Legendrepolynome und

$N_{lm} := \sqrt{\frac{2l+1}{2}\cdot\frac{(l-m)!}{(l+m)!}}$

sind Normierungsfaktoren. Mitunter ist die Berechnung über:

$P_{lm} (x)=(1-x^2)^{\frac{\left|m\right|}{2}} \left(\frac{\partial}{\partial x}\right)^{\left|m\right|} P_l(x)$

mit

$P_l (x)=\frac {1}{2^l}\sum_{k=0}^{\lfloor l/2\rfloor} (-1)^k \frac{(2l-2k)!}{k!(l-k)!(l-2k)!} x^{l-2k}$

vorteilhafter ( $\lfloor l/2\rfloor:={\mathrm{abrunden}}(l/2)$), da l-faches Ableiten entfällt.

Eine andere Definition geht über homogene, harmonische Polynome. Diese sind durch ihren Wert auf der Sphäre eindeutig bestimmt. Jedes homogene harmonische Polynom vom Grad n lässt sich als Linearkombination von Kugelflächenfunktionen multipliziert mit rⁿ schreiben und umgekehrt. Wählt man beispielsweise die Funktion, die konstant 1 ist, als Basis des eindimensionalen Vektorraumes der 0-homogenen harmonischen Polynome und x, y und z als Basis des dreidimensionalen Vektorraumes der 1-homogenen, so erhält man in Kugelkoordinaten nach Division von rⁿ die Funktionen

$1 \frac{}{}$

$\cos{\varphi} \sin \vartheta = \Re{(e^{i\varphi})} \sin \vartheta$,

$\sin \varphi \sin \vartheta = \Im{(e^{i\varphi})} \sin \vartheta$,

$\cos \vartheta \frac{}{}$.

Für die homogenen Polynome vom Grad 2 erkennt man in der Liste unten schnell auch die Terme $x^2-y^2, xy, x^2+y^2-2 z^2\frac{}{}$ wieder, nur mit einem falschen Vorfaktor.

Eigenschaften

Darstellung der Kugelflächenfunktionen

Die Kugelflächenfunktionen haben folgende Eigenschaften:

• Orthogonalitätsrelation: (δ_ij ist das Kronecker-Delta)

$\begin{align} &\int Y_{lm}^{*}(\vartheta,\varphi) \, Y_{l'm'}(\vartheta,\varphi) d\Omega \\ &\quad = \int_{0}^{2\pi} \int_{0}^{\pi} Y_{lm}^{*}(\vartheta,\varphi) \, Y_{l'm'}(\vartheta,\varphi) \, \sin{\vartheta} \, d\vartheta \, d\varphi \\ &\quad = \delta_{l\,l'} \, \delta_{mm'}\\ \end{align}$

• Vollständigkeit: (δ(x) ist die Delta-Distribution)

$\sum_{l=0}^{\infty}\sum_{m=-l}^{l}Y_{lm}^{*}(\vartheta ',\varphi ') \, Y_{lm}(\vartheta,\varphi) = \delta(\varphi-\varphi ')\delta(cos{\vartheta} -cos{\vartheta '})$

• Parität: Der Übergang $\vec r \rightarrow -\vec r$ sieht in Kugelkoordinaten folgendermaßen aus: $(r,\vartheta,\varphi) \rightarrow (r,\pi-\vartheta,\pi+\varphi)$. Unter dieser Transformation verhalten sich die Kugelflächenfunktionen wie folgt:

$Y_{lm}(\pi-\vartheta,\pi+\varphi)=(-1)^l\cdot Y_{lm}(\vartheta,\varphi)$

• Komplexe Konjugation: Die jeweiligen Y_{l, − m} erhält man aus den Y_lm durch:

$Y_{l,-m}(\vartheta,\varphi)=(-1)^m\cdot Y_{lm}^*(\vartheta,\varphi)$

Entwicklung nach Kugelflächenfunktionen

Die Kugelflächenfunktionen bilden ein vollständiges Funktionensystem. Daher können alle quadratintegrablen Funktionen $f(\vartheta,\varphi)$ (mit $\vartheta$ und φ im Sinne der Kugelkoordinaten) nach den Kugelflächenfunktionen entwickelt werden:

$f(\vartheta,\varphi)=\sum_{l=0}^\infty\sum_{m=-l}^{+l}c_{lm}Y_{lm}(\vartheta,\varphi)$

Die Entwicklungskoeffizienten c_lm berechnen sich zu:

$c_{lm}=\int_{\varphi=0}^{2\pi}\int_{\vartheta=0}^\pi Y_{lm}^*(\vartheta,\varphi)\cdot f(\vartheta,\varphi)\cdot\sin \vartheta \, d\vartheta \, d\varphi$

Dabei ist $Y_{lm}^*(\vartheta,\varphi)$ das komplex-konjugierte zu $Y_{lm}(\vartheta,\varphi)$. Die Darstellung einer Funktion f(x) mit sin - und cos -Funktion als Fourierreihe ist ein Analogon zur Entwicklung einer zweidimensionalen Funktion $f(\vartheta,\varphi)$ mit $Y_{lm}(\vartheta,\varphi)$ auf einer Kugeloberfläche.

Die ersten Kugelflächenfunktionen

Die ersten Kugelflächenfunktionen

Ylm	l = 0	l = 1	l = 2	l = 3
m = -3				$\sqrt{\tfrac{35}{64 \pi}} \sin^{3}{\vartheta}\,e^{-3i \varphi}$
m = −2			$\sqrt{\tfrac{15}{32 \pi}} \sin^{2}{\vartheta} \, e^{-2i \varphi}$	$\sqrt{\tfrac{105}{32\pi}} \sin^{2}{\vartheta}\cos{\vartheta}\,e^{-2i \varphi}$
m = −1		$\sqrt{\tfrac{3}{8 \pi}} \sin{\vartheta} \, e^{-i \varphi}$	$\sqrt{\tfrac{15}{8 \pi}} \sin{\vartheta} \, \cos{\vartheta} \, e^{-i \varphi}$	$\sqrt{\tfrac{21}{64 \pi}} \sin{\vartheta}\left( 5 \cos^{2}{\vartheta} - 1\right)\,e^{-i \varphi}$
m = 0	$\sqrt{\tfrac{1}{4 \pi}}$	$\sqrt{\tfrac{3}{4 \pi}} \cos{\vartheta}$	$\sqrt{\tfrac{5}{16 \pi}} \left( 3 \cos^{2}{\vartheta} - 1 \right)$	$\sqrt{\tfrac{7}{16 \pi}} \left( 5 \cos^{3}{\vartheta} - 3 \cos{\vartheta}\right)$
m = 1		$-\sqrt{\tfrac{3}{8 \pi}} \sin{\vartheta} \, e^{i \varphi}$	$-\sqrt{\tfrac{15}{8 \pi}} \sin{\vartheta} \, \cos{\vartheta} \, e^{i \varphi}$	$-\sqrt{\tfrac{21}{64\pi}} \sin{\vartheta}\left( 5 \cos^{2}{\vartheta} - 1\right)\,e^{i \varphi}$
m = 2			$\sqrt{\tfrac{15}{32 \pi}} \sin^{2}{\vartheta} \, e^{2i \varphi}$	$\sqrt{\tfrac{105}{32 \pi}} \sin^{2}{\vartheta}\cos{\vartheta}\,e^{2i \varphi}$
m = 3				$-\sqrt{\tfrac{35}{64 \pi}} \sin^{3}{\vartheta}\,e^{3i \varphi}$

Nomenklatur in der Geophysik

Kugelflächenfunktion werden auch gerne in der Geophysik verwendet. Man unterscheidet hier zwischen:

• zonal (m = 0): unabhängig von Längengrad φ
• sektoriell (m = l):

$Y_{ll}(\vartheta,\varphi) := \frac{(-1)}{l!}^l\sqrt{\frac{(2l+1)!}{4^{l+1}\pi}} \sin^l \vartheta e^{i l \varphi}$

• tesseral (sonst): längen- und breitengradabhängig

Literatur

• Eduard Heine Handbuch der Kugelfunctionen Georg Reimer, Berlin, 1861.
• A. Wangerin Theorie Des Potentials Und Der Kugelfunktionen II Band Walter de Gruyter, Berlin, 1921. (University of Michigan)
• Claude Cohen-Tannoudji, Bernard Diu und Franck Laloë: Quantenmechanik 1. 2. Auflage, Walter de Gruyter, Berlin - New York 1999, S. 649 ff.
• Torsten Fließbach: Elektrodynamik. 4. Auflage, Spektrum, München 2005, S. 99 ff.
• Otto Forster: Analysis 3. 3. Auflage, Vieweg Studium, 1984

Weblinks

• Applet zur Veranschaulichung der Kugelflächenfunktionen (englisch)