Eisenstein-Zahl — Eisenstein Zahlen als Punkte eines Dreiecksgitters in der komplexen Zahlenebene Die Eisenstein Zahlen sind eine Verallgemeinerung der ganzen Zahlen auf die komplexen Zahlen. Sie sind nach dem deutschen Mathematiker Gotthold Eisenstein, einem… … Deutsch Wikipedia
Eisenstein — Als Eisenstein werden eisenhaltige Sedimentgesteine bzw. Eisenerze bezeichnet, etwa: Magnetit, Magneteisenstein Limonit, Brauneisenstein oder Toneisenstein Hämatit, Roteisenstein Raseneisenstein Eisenstein ist daneben der Name folgender Orte:… … Deutsch Wikipedia
Irreelle Zahlen — ℂ Die komplexen Zahlen erweitern den Zahlenbereich der reellen Zahlen derart, dass auch Wurzeln negativer Zahlen berechnet werden können. Dies gelingt durch Einführung einer neuen Zahl i derart, dass i2 = − 1 ist. Diese Zahl i wird auch als… … Deutsch Wikipedia
Komplexe Zahlen — ℂ Die komplexen Zahlen erweitern den Zahlenbereich der reellen Zahlen derart, dass auch Wurzeln negativer Zahlen berechnet werden können. Dies gelingt durch Einführung einer neuen Zahl i derart, dass i2 = − 1 ist. Diese Zahl i wird auch als… … Deutsch Wikipedia
Ganze Zahlen — ℤ Die ganzen Zahlen sind eine Erweiterung der natürlichen Zahlen. Die ganzen Zahlen umfassen alle Zahlen …, −3, −2, −1, 0, 1, 2, 3, … und enthalten damit alle natürlichen Zahlen sowie deren Gegenzahlen. Die Menge der ganzen Zahlen wird mit dem… … Deutsch Wikipedia
Gotthold Eisenstein — Ferdinand Gotthold Max Eisenstein (* 16. April 1823 in Berlin; † 11. Oktober 1852 ebenda) war ein deutscher Mathematiker, der hauptsächlich in der Zahlentheorie und über elliptische Funktionen arbeitete … Deutsch Wikipedia
Gauß'sche Zahlen — Gaußsche Zahlen als Gitterpunkte in der komplexen Zahlenebene Die Gaußschen Zahlen (nach Carl Friedrich Gauß) sind eine Verallgemeinerung der ganzen Zahlen in den komplexen Zahlen. Sie werden auch mit bezeichnet (siehe … Deutsch Wikipedia
Gaußsche Zahlen — als Gitterpunkte in der komplexen Zahlenebene Die Gaußschen Zahlen (nach Carl Friedrich Gauß) sind eine Verallgemeinerung der ganzen Zahlen in den komplexen Zahlen. Sie werden auch mit bezeichnet (siehe … Deutsch Wikipedia
Gaußsche ganze Zahlen — Gaußsche Zahlen als Gitterpunkte in der komplexen Zahlenebene Die Gaußschen Zahlen (nach Carl Friedrich Gauß) sind eine Verallgemeinerung der ganzen Zahlen in den komplexen Zahlen. Sie werden auch mit bezeichnet (siehe … Deutsch Wikipedia
Heegner-Zahlen — Die Heegner Zahlen sind die neun Zahlen 1, 2, 3, 7, 11, 19, 43, 67 und 163. Sie sind nach Kurt Heegner benannt. Bedeutung der Heegner Zahlen In den gaußschen Zahlen und in den Eisenstein Zahlen ist die Primfaktorzerlegung im Wesentlichen… … Deutsch Wikipedia
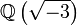 . Sie treten beispielsweise bei der Formulierung des kubischen Reziprozitätsgesetzes auf.
. Sie treten beispielsweise bei der Formulierung des kubischen Reziprozitätsgesetzes auf.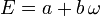 mit
mit 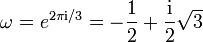
 ) definieren und zeigen, dass die Primfaktordarstellung einer Eisenstein-Zahl eindeutig ist. Ganze Zahlen der Form m2 + 3n2 sind in den Eisenstein-Zahlen immer zerlegbar. Daher sind die Zahlen 3, 7, 13, 19, ... keine Primelemente in den Eisenstein-Zahlen.
) definieren und zeigen, dass die Primfaktordarstellung einer Eisenstein-Zahl eindeutig ist. Ganze Zahlen der Form m2 + 3n2 sind in den Eisenstein-Zahlen immer zerlegbar. Daher sind die Zahlen 3, 7, 13, 19, ... keine Primelemente in den Eisenstein-Zahlen.
