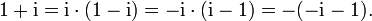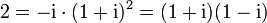- Gaußsche Zahlen
-
Die Gaußschen Zahlen (nach Carl Friedrich Gauß) sind eine Verallgemeinerung der ganzen Zahlen in den komplexen Zahlen. Sie werden auch mit
![\mathbb Z[\mathrm i]](/pictures/dewiki/57/98c48d82daf4a6005c90888df07977a1.png) bezeichnet (siehe Adjunktion (Algebra)). Jede gaußsche Zahl liegt auf einem ganzzahligen Koordinatenpunkt der komplexen Ebene. Die Gaußschen Zahlen bilden den Ganzheitsring des quadratischen Zahlkörpers
bezeichnet (siehe Adjunktion (Algebra)). Jede gaußsche Zahl liegt auf einem ganzzahligen Koordinatenpunkt der komplexen Ebene. Die Gaußschen Zahlen bilden den Ganzheitsring des quadratischen Zahlkörpers 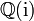 und insbesondere einen ZPE-Ring. Sie treten beispielsweise bei der Formulierung des biquadratischen Reziprozitätsgesetzes auf. Eine etwas kompliziertere Verallgemeinerung ganzer Zahlen, die auch in die komplexe Ebene eingebettet werden können, sind die Eisenstein-Zahlen.
und insbesondere einen ZPE-Ring. Sie treten beispielsweise bei der Formulierung des biquadratischen Reziprozitätsgesetzes auf. Eine etwas kompliziertere Verallgemeinerung ganzer Zahlen, die auch in die komplexe Ebene eingebettet werden können, sind die Eisenstein-Zahlen.Definition
Eine gaußsche Zahl g ist durch
- g = a + bi
gegeben, wobei a und b ganze Zahlen sind.
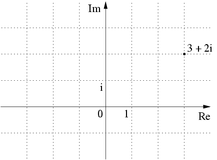
Die gaußschen Zahlen sind die Punkte mit ganzzahligen Koordinaten in der gaußschen Zahlenebene. Sie bilden ein zweidimensionales Gitter.
Primelemente
 Das Spektrum von
Das Spektrum von![\mathbb{Z}[\mathrm{i}]](/pictures/dewiki/54/60099e0f9a81595f1f7fec0f55da745a.png) veranschaulicht diese Zusammenhänge: Die Kleckse entsprechen den Primelementen im Ring der Gaußschen Zahlen, die in der Faktorisierung der jeweils unten angegebenen Primzahl auftauchen.
veranschaulicht diese Zusammenhänge: Die Kleckse entsprechen den Primelementen im Ring der Gaußschen Zahlen, die in der Faktorisierung der jeweils unten angegebenen Primzahl auftauchen.Mit den Gaußschen Zahlen lässt sich Zahlentheorie studieren. Im Besonderen lassen sich Primelemente als Verallgemeinerung des Begriffes Primzahl definieren. Die Eindeutigkeit der Primfaktordarstellung gilt dann auch für die Gaußschen Zahlen.
Die Primelemente im Ring der Gaußschen Zahlen haben einen engen Bezug zu den gewöhnlichen Primzahlen. Sie zerfallen in drei Klassen (jeweils bis auf Multiplikation mit
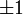 und
und 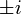 , den Einheiten des Ringes der Gaußschen Zahlen):
, den Einheiten des Ringes der Gaußschen Zahlen):- Der doppelte Primfaktor von 2: Die Zahl 2 kann als Produkt der Primelemente 1 + i und 1 − i geschrieben werden, die sich aber eben nur um eine Einheit unterscheiden (2 ist verzweigt):
-
- Also ist
- die Primfaktorzerlegung der Zahl 2 im Ring der gaußschen Zahlen, sie ist eindeutig, aber es kann keiner Darstellung der Vorzug gegeben werden, da die komplexen Zahlen und damit auch die gaußschen Zahlen und deren Einheiten nicht angeordnet werden können.
- Faktoren von Primzahlen der Form 4k + 1: Ist p eine Primzahl, die die Form p = 4k + 1 mit einer ganzen Zahl k hat, so kann man zeigen, dass sich p auf im wesentlichen eindeutige Weise als Summe zweier Quadratzahlen schreiben lässt:
-
- p = a2 + b2 mit gewissen
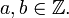
- p = a2 + b2 mit gewissen
- Dann ist
- p = (a + bi)(a − bi)
- die Primfaktorzerlegung von p, p selbst ist also kein Primelement im Ring der gaußschen Zahlen, sondern Produkt von zwei zueinander konjugierten Primelementen (p ist zerlegt). Beispielsweise ist 5 = (2 + i)(2 − i) keine Primzahl, aber 2 + i und 2 − i sind zwei Primelemente.
- Primzahlen der Form 4k + 3: Ist p eine Primzahl der Form 4k + 3 mit einer ganzen Zahl k, so ist p auch im Ring der gaußschen Zahlen ein Primelement (p bleibt prim; es ist träge).
Wikimedia Foundation.