Euler-Maruyama-Schema

Das Euler-Maruyama-Verfahren, oft auch Euler-Maruyama-Schema oder stochastisches Euler-Schema genannt, ist das einfachste Verfahren zur numerischen Lösung von stochastischen Differentialgleichungen. Es wurde erstmals in den 1950er-Jahren durch den japanischen Mathematiker Gisiro Maruyama untersucht und basiert auf dem von Leonhard Euler stammenden expliziten Euler-Verfahren zur Lösung gewöhnlicher (deterministischer) Differentialgleichungen.

Während das explizite Euler-Verfahren seit seiner Erfindung ständig verbessert und weiterentwickelt wurde (implizites Euler-Verfahren, Runge-Kutta-Verfahren, Mehrschrittverfahren) und selbst dadurch an praktischer Bedeutung verloren hat, ist Euler-Maruyama mangels entsprechender Alternativen noch immer das in der Praxis dominierende Verfahren.

Formulierung

Gegeben sei ein Wiener-Prozess 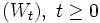$(W_t),\;t \ge 0$ sowie dazu folgendes stochastisches Anfangswertproblem (S-AWP):

$dS_t = a(t,S_t)dt + b(t,S_t)dW_t, \;\;S_0=A$.

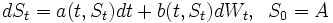Die Idee von Maruyama besteht nun darin, nicht nur (wie bei Euler) die Zeitachse in ein Gitter 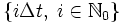$\{ i\Delta t, \; i \in \N_0\}$zu unterteilen, sondern diese Unterteilung auch in der Wahrscheinlichkeitsachse vorzunehmen: dazu definiert man

$\Delta W_i :=W_{i \Delta t}-W_{(i-1)\Delta t}, \; i \in \N$.

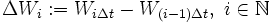Auf diesem Gitter berechnet sich die Approximation 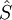$\hat{S}$ von S folgendermaßen:

$\hat{S}_0=A, \;\;\hat{S}_{i \Delta t} = \hat{S}_{(i-1)\Delta t} + a((i-1)\Delta t,\hat{S}_{(i-1)\Delta t}) \Delta t + b((i-1)\Delta t,\hat{S}_{(i-1)\Delta t}) \Delta W_i$.

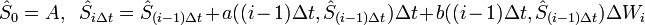Konvergenz des Verfahrens

Das wichtigste theoretische Resultat bezüglich des Maruyama-Schemas beschreibt dessen starke Konvergenz (oder stochastische Konvergenz) gegen die gesuchte Lösung S: eine Folge von stochastischen Prozessen 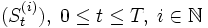$(S_t^{(i)}),\;0 \le t \le T, \;i \in \N$ auf einem gemeinsamen Wahrscheinlichkeitsraum konvergiert definitionsgemäß stark mit Ordnung q gegen einen Prozess 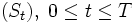$(S_t), \;0 \le t \le T$, wenn für eine Konstante c gilt:

$E(|S_t^{(i)}-S_t|) \le c i^{-q} \;\;\forall t \in [0,T]$.

Im Falle des Maruyama-Schemas kann nun gezeigt werden: die Diskretisierung 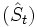$(\hat{S}_t)$ konvergiert für 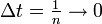$\Delta t = \tfrac{1}{n} \to 0$ stark mit Ordnung 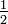$\tfrac{1}{2}$ gegen die Lösung S des S-AWP, wenn für alle reellen Zahlen x und alle positiven s,t die folgende Schranke gilt:

$|a(s,x)-a(t,x)| + |b(s,x)-b(t,x)| \le K(1+|x|)\sqrt{(|t-s|)}$.

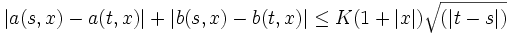Von schwacher oder Verteilungskonvergenz mit Ordnung q spricht man hingegen, wenn für eine Konstante c gilt:

$|E(f(S_t^{(i)}))-E(f(S_t))| \le c n^{-q} \;\;\forall t \in [0,T]$

für alle Funktionen f, die mindestens (2q + 2)-mal stetig differenzierbar sind und deren sämtliche Ableitungen durch Polynome beschränkt sind. Dies ist bei Maruyama dann der Fall, wenn die Funktionen a und b diese Bedingung ebenfalls erfüllen. Für hinreichend glatte Funktionen a und b kann das Euler-Maruyama also beliebig hohe schwache Konvergenzordnung erreichen, jedoch ist dabei nichts über die Konstante c ausgesagt (diese können analog zur Konvergenzordnung gegen Unendlich gehen.)

Bemerkungen

• Es gibt auch Lösungsverfahren höherer starker Ordnung als das Euler-Maruyama-Verfahren, etwa das Milstein-Verfahren, das meist Ordnung 1 erreicht. Diese Verfahren sind aber numerisch aufwändiger und resultieren nicht immer in einer schnelleren Konvergenz.

• Die oben angeführte Bedingung für die starke Konvergenz mit Ordnung 0.5 ist nur wenig strenger als die Bedingung an a und b, die die Existenz der Lösung S sicherstellt. Sie ist also beinahe immer erfüllt.

• An starker Konvergenz ist man in der Praxis nur sehr selten interessiert, da zumeist nicht eine spezielle Lösung zu einem speziellen Wiener-Prozess gesucht wird, sondern Vielmehr eine Stichprobe aus der Wahrscheinlichkeitsverteilung des Prozesses.

• Ein Implizites Maruyama-Schema als Analogon zum impliziten Euler-Verfahren ist nicht möglich; dies liegt an der Definition des (stochastischen) Ito-Integrals, über das stochastische Differentialgleichungen definiert sind und das Funktionen immer am Anfang eines Intervalls auswertet (siehe dort). Implizite Verfahren konvergieren also hier gegen teilweise völlig falsche Ergebnisse.

• Die übliche Simulation einer brownschen Bewegung durch einen gaußschen Random Walk kann als Anwendung des Euler-Maruyama-Schemas auf die triviale Differentialgleichung 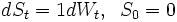$dS_t =1 dW_t, \;\;S_0=0$ interpretiert werden.

Literatur

• Paul Glasserman: Monte Carlo Methods in Financial Engineering, Springer 2003, ISBN 0-387-00451-3