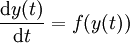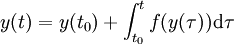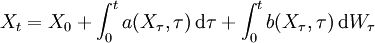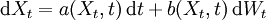SDGL

Der Begriff der stochastischen Differentialgleichung (Abkürzung SDGL oder englisch SDE für stochastic differential equation) verallgemeinert den Begriff der gewöhnlichen Differentialgleichung auf stochastische Prozesse. Schon allein die mathematische Formulierung des Problems stellte die Mathematiker vor große Probleme (siehe unten), und so wurde die formale Theorie der stochastischen Differentialgleichungen erst in den 1940er Jahren durch den japanischen Mathematiker Itō Kiyoshi formuliert. Gemeinsam mit der stochastischen Integration begründet die Theorie der stochastischen Differentialgleichungen die stochastische Analysis.

Stochastische Differentialgleichungen werden auf verschiedenen Feldern der mathematischen Modellierung verwendet, um gewöhnliche (d.h. deterministische, vorhersehbare) Prozesse zu simulieren, die zusätzlich von außen durch stochastische Störfaktoren (Rauschen) beeinflusst werden.

Von der Differential- zur Integralgleichung

Genau wie bei deterministischen Funktionen möchte man auch bei stochastischen Prozessen den Zusammenhang zwischen dem Wert der Funktion und ihrem zukünftigen Verlauf (ihrer Ableitung) in einer Gleichung formulieren. Was im einen Fall zu einer gewöhnlichen Differentialgleichung führt, ist im anderen Fall problematisch, da Itô-Prozesse im Allgemeinen nirgends differenzierbar (ableitbar) sind.

Jedoch lässt sich eine (autonome) Differentialgleichung

$\frac{{\rm d}y(t)}{{\rm d}t} = f(y(t))$

immer auch äquivalent als Integralgleichung

$y(t) = y(t_0) + \int_{t_0}^t f(y(\tau)){\rm d}\tau$

schreiben, die ohne explizite Erwähnung der Ableitung auskommt. Bei der stochastischen Differentialgleichung geht man nun den umgekehrten Weg, d.h., man erklärt eine Differentialgleichung anhand der dazugehörigen Integralgleichung.

Die Formulierung

Seien zwei Funktionen 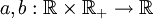$a,b:\mathbb{R} \times \mathbb{R}_{+} \to \mathbb{R}$ sowie eine brownsche Bewegung 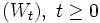$(W_t), \; t \ge 0$ gegeben. Die dazugehörige stochastische Integralgleichung

$X_t=X_0 + \int_0^t a(X_\tau,\tau) \,{\rm d}\tau + \int_0^t b(X_\tau,\tau)\,{\rm d}W_\tau$

wird durch Einführung der Differentialschreibweise

${\rm d} X_t=a(X_t,t)\,{\rm d}t+b(X_t,t)\,{\rm d}W_t$

zur stochastischen Differentialgleichung. Das erste Integral ist als Lebesgue-Integral und das zweite als Itô-Integral zu lesen. Zu gegebenen Funktionen a und b (auch als Drift und Diffusion bezeichnet) und einer speziellen brownschen Bewegung W wird hier also ein Prozess X gesucht, der zusammen mit a, b und W die obige Integralgleichung erfüllt. Dieser Prozess ist dann eine Lösung der obigen SDE.

Existenz und Eindeutigkeit

Ist A eine beliebige, auf demselben Wahrscheinlichkeitsraum wie W definierte Zufallsvariable, so wird aus der obigen SDGL durch Hinzufügen der Bedingung X₀ = A f.s. ein stochastisches Anfangswertproblem als Pendant zum Anfangswertproblem für gewöhnliche Differentialgleichungen.

Auch zum Existenz- und Eindeutigkeitssatz von Picard und Lindelöf findet sich hier eine Entsprechung: wenn die folgenden zwei Eigenschaften erfüllt sind:

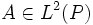• $A \in L^2(P)$, d.h., A hat endliche Varianz.
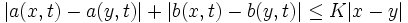
• Es gibt eine Konstante K, sodass 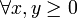$|a(x,t)-a(y,t)|+|b(x,t)-b(y,t)| \le K|x-y|$ $\forall x,y \ge 0$ (Lipschitz-Bedingung).

Dann besitzt das Anfangswertproblem eine (bis auf fast sichere Gleichheit) eindeutige Lösung X, die zudem zu jedem Zeitpunkt t endliche Varianz besitzt.

Beispiele

• Die Black-Scholes-Differentialgleichung für die geometrische brownsche Bewegung: dS_t = rS_tdt + σS_tdW_t
• Die SDE für den Wurzel-Diffusionsprozess nach William Feller lautet ${\rm d}X_t = \kappa (\theta - X_t){\rm d}t+ \sigma \sqrt{X_t}{\rm d}W_t$

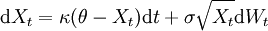
Lösen von stochastischen Differentialgleichungen und Simulation der Lösungen

Genau wie bei deterministischen gibt es auch bei stochastischen Differentialgleichungen keinen allgemeinen Ansatz zur Ermittlung der Lösung. In manchen Fällen (wie bei der oben erwähnten Black-Scholes-SDE, deren Lösung eine geometrische brownsche Bewegung ist) ist es auch hier möglich, die Lösung zu „erraten“ und durch Ableiten zu verifizieren (wobei das Differenzieren hier mit Hilfe des Lemmas von Itō erfolgt).

In den meisten Fällen, die in der Praxis auftauchen, wie zum Beispiel auch im Fall des Wurzel-Diffusionsprozesses, ist jedoch keine geschlossene Form der Lösung zu erreichen. Doch ist man zumeist auch nur daran interessiert, Zufallspfade der entsprechenden Lösung zu simulieren. Dies kann approximativ durch numerische Diskretisierungsvefahren erreicht werden, etwa durch das Euler-Maruyama-Schema (das dem expliziten Euler-Verfahren für gewöhnliche Differentialgleichungen nachempfunden ist) oder das Milstein-Verfahren.