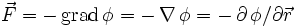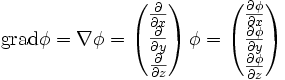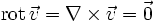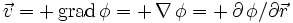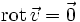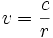Strömungspotenzial

Potentialströmung wird die Strömung eines Fluids (Flüssigkeit oder Gas) genannt, wenn das Vektorfeld der Geschwindigkeiten mathematisch so geartet ist, dass es ein Potentialfeld (Potential) besitzt. Eine solche Strömung ist in einem homogenen Fluid vorhanden, wenn es rotationsfrei (wirbelfrei) ist und keine Zähigkeitskräfte (Reibungskräfte) auftreten oder diese vernachlässigbar klein sind. Jede aus der Ruhe heraus beginnende Strömung eines homogenen, reibungsfreien Fluids besitzt ein solches Potential. Potentialströmung ist ein Spezialfall der durch die Eulerschen Bewegungsgleichungen beschriebenen Hydrodynamik einer idealen Flüssigkeit.

Kraftpotential (Beschleunigungspotential)

Der mathematische Begriff Potential hat seinen Ursprung in der Physik der konservativen Kraftfelder. Dort ist das Potential die Fähigkeit eines Feldes, Arbeit pro Massen- oder Ladungseinheit zu verrichten (potentielle Energie pro Masse bzw. Ladung). Das Potential beschreibt dort also die Wirkung des Kraftfeldes auf Massen oder Ladungen, unabhängig von der Größe dieser Massen oder Ladungen.

Im folgenden wird das jeweilige Potential (es sind verschiedene) mit dem griechischen Buchstaben 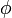$\phi\!$ (Phi) bezeichnet.

Das Kraftfeld 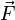$\vec F\!$ = (F_x, F_y, F_z), ein dreidimensionales Vektorfeld, erhält man durch partielle Ableitung des Potentials nach dem Ort (Position), also aus der räumlichen Änderung des Potentials:

$\vec F = -\,\mbox{grad}\,\phi = -\,\nabla\,\phi = -\,\partial\,\phi/\partial\vec r$

wobei der Operator grad (Gradient) oder $\nabla$ (der Nabla-Operator) in kartesischen Koordinaten

$\operatorname{grad}\phi = \nabla\phi = \begin{pmatrix} \frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \\ \frac{\partial}{\partial z} \end{pmatrix} \,\phi = \begin{pmatrix} {\frac{\partial \phi}{\partial x}} \\ {\frac{\partial \phi}{\partial y}} \\ {\frac{\partial \phi}{\partial z}} \end{pmatrix}$

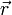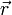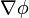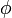bedeutet. $\vec r\!$ ist hier der Ortsvektor, der den Ort im Raum (die Position) angibt. Die Ableitung nach $\vec r\!$ bei der Bildung des Gradienten $\nabla\phi\!$ von $\phi\!$ symbolisiert dabei eine Ableitung nach allen Komponenten (Koordinaten) von 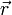$\vec r\!$. Im eindimensionalen Fall ist der Gradient die gewöhnliche Ableitung nach dem Weg in Richtung dieser Dimension.

Geschwindigkeitspotential

Anders als das Potential eines Kraftfeldes ist das Geschwindigkeitspotential oder Strömungspotential nicht die Fähigkeit (potentielle Energie) eines Feldes, Arbeit zu verrichten. Das Potential 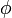$\phi\!$ des Geschwindigkeitsfeldes $\vec v$ beschreibt eine spezielle innere Ordnung dieses Feldes, die mathematisch (formal) die Struktur der konservativen Kraftfelder ist, jedoch physikalisch etwas anderes darstellt, nämlich Rotationslosigkeit (keine Vorticity):

$\mbox{rot}\, \vec{v}=\nabla\times\vec{v}=\vec{0}$

Da das Geschwindigkeitspotential keine potentielle Energie beinhaltet, ist das Vorzeichen nicht festgelegt und wird gewöhnlich positiv definiert:

$\vec v = +\,\mbox{grad}\,\phi = +\,\nabla\,\phi = +\,\partial\,\phi/\partial\vec r$

In der Potentialströmung gilt die Bernoulli-Gleichung nicht nur entlang einer Stromlinie, sondern auch „quer“ dazu für die benachbarten Stromlinien, also für das ganze Gebiet der Potentialströmung. Die Eulerschen Bewegungsgleichungen sind die Bewegungsgleichungen der Hydrodynamik der idealen Fluide, zu der die Potentialströmungen gehören. Diese Bewegungsgleichungen gelten darüber hinaus auch für Strömungen homogener, reibungsfreier Fluide mit Rotation. Wenn jedoch die Zähigkeit berücksichtigt werden muss, wie beispielsweise in jeder Grenzschicht (Hydrodynamische Grenzschicht) und im Zentrum eines Wirbels, muss dagegen mit den Navier-Stokes-Gleichungen gerechnet werden und die Strömung ist keine Potentialströmung.

Der Gegensatz zur Potentialströmung ist also nicht nur die Wirbelströmung mit Vorticity (es existieren auch kreisende Potentialströmungen ohne Vorticity), sondern vor allem die nicht reibungsfreie Strömung, in der bei Scherbewegungen Zähigkeitskräfte auftreten.

Potentialströmung mit Zirkulation (Potentialwirbel)

Der Potentialwirbel oder „freie Wirbel“ ist eine kreisende und dennoch rotationsfreie Potentialströmung, bei der also die Rotation des Geschwindigkeitsfeldes

$\mbox{rot}\, \vec{v}=\vec{0}$

ist und die daher eine echte Potentialströmung darstellt, die in einem zweifach zusammenhängenden Gebiet (wie beispielsweise der Luftraum in einem Saal mit Mittelsäule) eine Zirkulation aufweist.

Freie Wirbel in realen Fluiden bilden diese Potentialströmung näherungsweise aus mit Ausnahme eines Kerngebietes in ihrer Mitte, wo Zähigkeitskräfte zu einer quasi-starren Rotation führen und das Geschwindigkeitsfeld Vorticity hat, also keine Potentialströmung darstellt. Beim freien Wirbel bewegen sich alle Fluidpartikel auf konzentrischen Kreisbahnen mit Geschwindigkeiten v, die (außer im Kerngebiet) dem Abstandsgesetz mit Konstante c und Achsenabstand r

$v=\frac{c}{r}$

entsprechen. Dadurch ist eine völlig andere Geschwindigkeits- und Druckverteilung als beim quasistarren Wirbel gegeben, der kein Potential besitzt und dessen Geschwindigkeit proportional zum Achsenabstand r ist.

Ein besonderer Potentialwirbel ist an einer freien Wasseroberfläche zu beobachten, wenn der Druck im Zentrum so gering wird, dass sich die Oberfläche merklich einsenkt und einen Wirbeltrichter (Strudel) bildet. Reicht der Trichter unbegrenzt weit in die Tiefe, herrscht im ganzen Flüssigkeitsgebiet Potentialströmung, nicht jedoch im luftgefüllten Kern.

Literatur

• Herbert Oertel (Hrg.): Prandtl-Führer durch die Strömungslehre. Grundlagen und Phänomene, Vieweg 2002 (11. Aufl), ISBN 3-528-48209-5
• Jürgen Zierep: Grundzüge der Strömungslehre, G. Braun Karlsruhe 1990, ISBN 3-7650-2039-7
• Hans J. Lugt: Wirbelströmung in Natur und Technik, G. Braun Karlsruhe 1979, ISBN 3-7650-2028-1