Evolvente

Die Evolvente ist ein Begriff aus dem mathematischen Teilgebiet Differentialgeometrie. Jeder rektifizierbaren Kurve wird eine Schar von anderen Kurven als deren Evolventen zugeordnet, die durch die „Abwicklung“ von deren Tangente entstehen.

Anschaulich lässt sich die Evolvente als Fadenlinie darstellen: Ein flacher Körper, dessen eine Seitenfläche die Form der Ausgangskurve hat, wird auf ein Blatt Papier gelegt. Über die Ausgangskurve ist ein dünner Faden straff gespannt. Am äußeren Ende des Fadens wird ein Stift befestigt, dessen Spitze auf dem Papier aufliegt. Dann wird der Faden langsam von der Kurve abgehoben, wobei er stets straff gehalten wird. Die Kurve, die auf dem Papier entsteht, ist eine Evolvente.

Da der Faden anfangs eine beliebige Länge haben kann, gibt es zu jeder Kurve unendlich viele Evolventen, die alle parallel zueinander verlaufen, das heißt: Sind zwei Evolventen gegeben, so ist jede Normale der einen auch Normale der anderen, und alle diese Normalen sind zwischen den beiden Evolventen gleich lang. Jede Normale einer Evolvente ist also Normale aller Evolventen. Die Normalen der Evolventen sind einfach die Tangenten der gegebenen Kurve. Diese ist Hüllkurve (Enveloppe) der Evolventennormalen. Meist ist mit Evolvente die Kreisevolvente gemeint; dies ist jedoch nur ein Spezialfall der allgemeinen Evolvente.

Beispiel

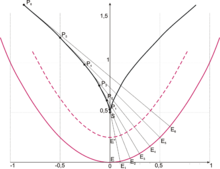
Als Ausgangskurve wird hier eine neilsche Parabel $y = \tfrac{1}{2}+3 \cdot \sqrt[3]{\tfrac{x^2}{16}}$ (schwarz gezeichnet) verwendet.

P₁E₁, P₂E₂,... (grau gezeichnet) sind Tangenten an die neilsche Parabel; SE ist eine linksseitige Tangente. Die Strecke $\overline {SE}$ hat hier die Länge 0,5. Die folgenden Strecken $\overline {P_1E_1}$, $\overline {P_2E_2}$,... übertreffen $\overline {SE}$ um die Länge des Bogens $\widehat {P_1S}$, $\widehat {P_2S}$,...
Die Endpunkte E₁, E₂,... der Tangentenabschnitte bilden die Evolvente der neilschen Parabel (violett gezeichnet), hier eine Normalparabel $y \, = \, x^2$. (Der linke Ast der Parabel entsteht, wenn die "Abwicklung" nach rechts erfolgt).
Wählt man für $\overline {SE}$ eine andere Länge als 0,5, so entstehen dazu parallele Parabeln als weitere Evolventen (gestrichelt). Eingezeichnet ist die Parabel zu $\overline {SE'} = 0{,}25$

Evolvente und Evolute

Die Ausgangskurve, aus der die Evolvente entsteht, heißt deren Evolute. Im obigen Beispiel ist die Evolute die Neilsche Parabel, bei der Kreisevolvente ist es der Kreis. Wegen dieser Wechselbeziehung wird die Evolvente zuweilen auch Involute genannt.

Anwendungen

In der Technik hat die Evolvente besonders bei der Konstruktion von Zahnrädern und Zahnstangen eine große Bedeutung. Bei der häufig angewandten Evolventenverzahnung ist der Querschnitt einer Zahnflanke Teil einer Evolvente. Dadurch wird gewährleistet, dass sich im Eingriff stehende Zähne entlang einer geraden Eingriffslinie (der Tangente an die Grundkreise) berühren. Die Evolventenform ist dabei einfacher zu fertigen als die ebenfalls verwendete Zykloidenform der Zahnflanke.