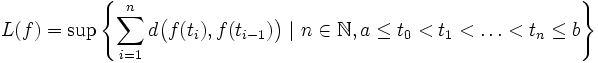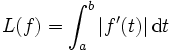Rektifizierbar

In der Topologie und der Analysis ist ein Weg eine stetige Abbildung eines reellen Intervalls in einen topologischen Raum. Das Bild eines Weges heißt Kurve.

Definition

Sei X ein topologischer Raum, I = [a,b] ein reelles Intervall. Ist 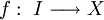$f: \ I \longrightarrow X$ eine stetige Funktion, dann heißt f ein Weg in X. Die Bildmenge f(I) heißt Kurve in X.

Die Punkte f(a) und f(b) heißen Anfangspunkt und Endpunkt der Kurve.

Ein Weg f heißt geschlossener Weg, wenn f(a) = f(b) ist. Ein geschlossener Weg liefert eine stetige Abbildung vom Einheitskreis S¹ nach X. Einen geschlossenen Weg nennt man auch Schleife.

Ein Weg f heißt einfacher Weg (oder auch doppelpunktfrei), wenn f auf [a,b) injektiv ist. Insbesondere ist also f(a) = f(b) zugelassen. Ein einfacher Weg heißt auch Jordan-Weg.

Diese Definition umfasst das, was wir uns intuitiv unter einer „Kurve“ vorstellen: Eine zusammenhängende geometrische Figur, die „wie eine Linie“ ist (eindimensional). Aber es gibt auch Kurven, die nicht intuitiv so genannt werden würden.

Man muss zwischen einem Weg und einer Kurve (dem Bild eines Weges) unterscheiden. Zwei verschiedene Wege können dasselbe Bild haben. Oft sind wir jedoch nur an dem Bild interessiert, und nennen dann den Weg eine Parameterdarstellung der Kurve.

Wenn es zu einer Kurve eine Parametrisierung gibt, die ein Jordan-Weg ist, dann nennt man die Kurve eine Jordan-Kurve, ebenso für geschlossene Kurve.

Beispiele

Der Graph einer stetigen Funktion $h: \ [a,b] \longrightarrow X$ ist eine Jordan-Kurve in R×X. Eine Parametrisierung ist der Jordan-Weg $f: \ [a,b] \longrightarrow$ R×X, mit f(t) = (t,h(t)). Dabei wird auf R×X die Produkttopologie verwendet.

Der Einheitskreis ist eine geschlossene Jordan-Kurve.

Rektifizierbare Wege

Ist X ein metrischer Raum mit Metrik d, dann können wir die Länge L eines Weges f in X definieren:

$L(f) = \sup\left\{ \sum_{i=1}^n d \big(f(t_i),f(t_{i-1})\big)\ |\ n \in \mathbb{N}, a\le t_0 < t_1 < \ldots < t_n \le b\right\}$

Ein rektifizierbarer Weg ist ein Weg mit endlicher Länge.

Ist weiterhin 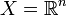$X=\mathbb{R}^n$, dann gilt:

Jeder stückweise stetig differenzierbare Weg ist rektifizierbar, und seine Länge ist das Integral über den Betrag der Ableitung:

$L(f) = \int_a^b |f'(t)| \,\mathrm{d}t$

Die Koch-Kurve und auch eine Trajektorie eines Wiener-Prozesses sind Beispiele für nicht rektifizierbare Wege.

Andere Wege

Ein fraktaler Weg ist ein Weg mit gebrochener Dimension. Da es verschiedene Definitionen der gebrochenen Dimension gibt, gibt es also auch verschiedene Definition eines fraktalen Wegs. Typische Beispiele sind die Koch-Kurve und die Drachenkurve.

Siehe auch

• Trajektorie (Physik)

Literatur

• Stefan Hildebrandt. Analysis 2. Springer 2003. 1.Auflage S.110 ff. ISBN 3-540-43970-6