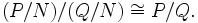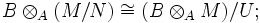Faktormodul

Im mathematischen Teilgebiet der Algebra ist ein Quotientenmodul oder Faktormodul eine der grundlegenden Konstruktionen der Theorie der Moduln. Zu einem Modul M und einem Untermodul 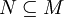$N\subseteq M$ ist der Quotientenmodul M / N das im wesentlichen eindeutig bestimmte Ziel eines surjektiven Homomorphismus $M\to M/N$ mit Kern N.

Quotientenmoduln sind das Analogon der Begriffe Faktorraum in der Theorie der Vektorräume sowie Faktorgruppe in der Gruppentheorie.

Definition

Es sei A ein Ring. Zu einem A-(Links-)Modul M und einem Untermodul 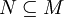$N\subseteq M$ ist der Quotientenmodul M / N die Menge der Äquivalenzklassen von Elementen von M nach der Äquivalenzrelation

$m_1\equiv m_2\mod N\iff m_1-m_2\in N$

mit der eindeutig bestimmten Modulstruktur, für die die kanonische surjektive Abbildung $M\to M/N$ ein Homomorphismus ist:

$a\cdot (m+N)=am+N.$

Eigenschaften

• Isomorphiesätze: Für zwei Untermoduln M,N eines Moduls Q gilt

$M/(M\cap N)\cong(M+N)/N.$

Für Untermoduln $N\subseteq Q\subseteq P$ gilt

$(P/N)/(Q/N)\cong P/Q.$

• Es gibt eine kanonische Entsprechung zwischen Isomorphieklassen von Monomorphismen mit Ziel M und Isomorphieklassen von Epimorphismen mit Quelle M; einem Monomorphismus $i\colon N\to M$ entspricht der Quotientenmodul M / i(N), einem Epimorphismus $p\colon M\to Q$ der Untermodul $\ker p$.
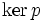• Ist ein Modul endlich erzeugt, oder hat er eine endliche Länge, so gilt dies auch für jeden Quotientenmodul.
• Ist B eine (unitäre, assoziative) A-Algebra, so ist

$B\otimes_A(M/N)\cong(B\otimes_AM)/U;$

dabei steht U für das Bild von $B\otimes_AN$ in $B\otimes_AM$.

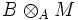• Ist I ein (zweiseitiges) Ideal in A, so ist der Faktormodul A / I dasselbe wie der Faktorring A / I.