- Fast Data Encipherment Algorithm
-
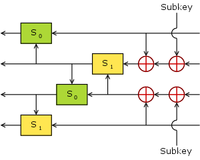
FEAL Eine Feistel-Runde von FEAL Entwickler Akihiro Shimizu und Shoji Miyaguchi, beide von NTT Veröffentlicht FEAL-4 1987; FEAL-N/NX 1990 Schlüssellänge 64 Bit (FEAL), 128 Bits (FEAL-NX) Blockgröße 64 Bit Struktur Feistelchiffre Runden Ursprünglich 4 bei FEAL-4, dann erweitert auf 8 Runden; FEAL-N/NX mit variabler Rundenanzahl, wobei minimal 32 empfohlen sind. Beste bekannte Kryptoanalyse FEAL-4 ist sehr anfällig für die lineare Kryptoanalyse mit nur fünf bekannten Klartextblöcken. (Matsui und Yamagishi, 1992).
FEAL-N/NX ist für die differentielle Kryptoanalyse mit weniger als 31 Runden anfällig. (Biham und Shamir, 1991).FEAL (Fast Data Encipherment Algorithm) ist ein Blockchiffre und zählt zu den symmetrischen Verschlüsselungsalgorithmen. Das Ziel bei der Entwicklung war, welche von dem japanischen Telefonkonzern Nippon Telegraph and Telephone (NTT) ausging, eine effiziente Implementierung eines Verschlüsselungsalgorithmus in Software auch für kleine Mikrocontroller zu erreichen und damit eine Alternative zu den von amerikanischen Behörden entwickelten Data Encryption Standard (DES) darzustellen. DES ist in Software nur vergleichsweise ineffizient zu implementieren.
FEAL diente in den Jahren nach seiner Entwicklung 1987 vor allem als Testobjekt für verschiedenartige Angriffszenarien auf Verschlüsselungsalgorithmen. Insbesondere diente er dazu um die heute wesentlichen Analyseverfahren, die differentielle Kryptoanalyse und die lineare Kryptoanalyse, in ihrer Entwicklung voran zu bringen. FEAL selber gilt, in den ursprünglichen Versionen wie FEAL-4 und FEAL-8, als gebrochen und sollte daher nicht eingesetzt werden.
Versionen
Ursprünglich wurde 1988 von dem Entwicklerteam um Akihiro Shimizu und Shoji Miyaguchi bei NTT FEAL-4 entwickelt. Dieser Algorithmus und seine Entstehungsgeschichte dokumentiert auch sehr anschaulich und mit teilweise amüsanten Abläufen die Problematik die mit der Entwicklung sicherer Blockverschlüsselungsalgorithmen verbunden sein kann.
Damit der Algorithmus in Software einen möglichst hohen Durchsatz erzielt, war die Anzahl der Runden nur auf vier festgelegt. FEAL-4 wurde noch im gleichen Jahr 1988 auf der Eurocrypt '88 von B. den Boer gebrochen[1]. Nur zwei Jahre später wurde von Sean Murphy die von ihm neu entwickelte differentielle Kryptoanalyse erfolgreich gegen FEAL-4 eingesetzt, wobei er nur 20 gewählte Klartextblöcke benötigte.[2]
Die Entwickler verbesserten darauf hin ihren Algorithmus und schufen im Jahr 1989 FEAL-8, eine Version mit acht Runden. Dieser Algorithmus wurde ebenfalls im gleichen Jahr von Biham und Shamir auf der Konferenz SECURICOM '89 erfolgreich kryptoanalysiert.
Die Entwickler sahen sich daraufhin gezwungen, ihr Ziel, mit möglichst wenigen Runden eine effiziente Softwareimplementierung zu erreichen, endgültig aufgeben zu müssen, und veröffentlichten FEAL-N mit einer variablen Anzahl von Runden. Auf der SECURICOM '91 konnte wieder von Biham und Shamir gezeigt werden, das FEAL-N für weniger als 32 Runden effizienter als mit Brute-Force geknackt werden kann.
Die Entwickler von FEAL entwarfen parallel im Jahr 1990 auch FEAL-NX, eine Variante, die mit 128 Bit langen Schlüsseln statt der ursprünglich gewählten 64 Bit langen Schlüsseln arbeitete. Sehr zum Leidwesen der Entwickler wurde auf der SECURICOM '91 von Biham und Shamir gezeigt, dass FEAL-NX mit 128 Bit langen Schlüssel genauso leicht zu brechen ist, wie FEAL-N mit 64 Bit langen Schlüsseln.
Darüber hinaus wurden von verschiedenen Entwicklungsteams Modifikationen zur Stärkung vorgeschlagen, wie FEAL-N(X)S, welche FEAL durch eine dynamische Vertauschungsfunktion stärken soll. Allerdings gehen alle diese Erweiterungen sehr zu Lasten des Datendurchsatzes.
FEAL wird vor allem zum Testen neuer und Verfeinern von kryptoanalytischen Angriffsmethoden verwendet. FEAL, egal in welcher Version, sollte wegen seiner bekannten Schwächen nicht in sicherheitskritischen Bereichen eingesetzt werden. FEAL ist weiters in den USA patentiert, das Patent läuft 2009 aus.
Referenzen
- ↑ B. den Boer: Cryptanalysis of F.E.A.L., Advances in Cryptology - EUROCRYPT '88 Proceesings, Springer Verlag, 1988, Seite 293-299
- ↑ Sean Murphy: The Cryptoanalysis of FEAL-4 with 20 Chosen Plaintexts, Journal of Cryptology, 1990, Seite 145 bis 155 ( http://www.springerlink.com/content/q14267573711682j/fulltext.pdf )
Wikimedia Foundation.