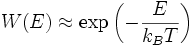- Fermiverteilung
-
Die Fermi-Verteilung folgt aus der Fermi-Dirac-Statistik im wichtigen Spezialfall der Wechselwirkungsfreiheit. Sie gibt unter dieser Zusatzvoraussetzung an, mit welcher Wahrscheinlichkeit ein Fermion eine Energie E zu gegebener Temperatur T hat. Die Verteilung ist nach dem italienischen Physiker Enrico Fermi benannt.
Inhaltsverzeichnis
Beschreibung
In einem System der Temperatur T lautet die Fermi-Verteilung wie folgt:
mit E der Energie, kB der Boltzmann-Konstante, T der Temperatur und μ das sog. chemische Potential. Letzteres ist im Wesentlichen durch die Teilchenzahl im System festgelegt (am Nullpunkt der absoluten Temperatur geht es in die Fermi-Energie Ef über).
Um die Besetzungszahl eines Energieniveaus zu berechnen, z. B. für Elektronen in einem Metall, muss die Fermi-Verteilung mit der Zustandsdichte D(E) multipliziert werden.
Das Fermi-Niveau ist im Bändermodell das zur Fermi-Energie Ef gehörende Energieniveau, das eine Besetzungswahrscheinlichkeit nach der Fermi-Dirac-Statistik von ½ besitzt. Für Metalle, bei denen das Fermi-Niveau im Leitungsband liegt, ist dies bei einer Temperatur von 0 Kelvin das höchste mit Elektronen besetzt Energieniveau; man spricht in dem Zusammenhang auch von Fermi-Grenze. Bei Isolatoren und Halbleitern liegt das Fermi-Niveau in der Bandlücke, dies führt dazu, dass bei einer Temperatur von 0 Kelvin das Valenzband vollständig mit Elektronen besetzt und das Leitungsband unbesetzt ist. Durch Einbringen zusätzlicher Ladungsträger (Donator- oder Akzeptordotierung) kann eine Verschiebung des Fermi-Niveaus erreicht werden. Neben der Störstellenkonzentration verschiebt auch die Temperatur das Niveau.
Fermi-Verteilung am absoluten Temperaturnullpunkt
Das Pauli-Prinzip besagt, dass Fermionen sich mindestens in einer Quantenzahl unterscheiden müssen. Dies hat zur Folge, dass auch am absoluten Temperaturnullpunkt Fermionen in angeregten Energiezuständen sitzen müssen. Anschaulich lässt sich das mit Vorstellung eines Fermi-Sees verstehen: Jedes hinzugefügte Fermion besetzt den tiefstmöglichen Energiezustand, welcher noch nicht von einem anderen Fermion besetzt ist. Die Fermi-Verteilung hat bei T = 0 K also eine scharfe Kante bei einer Energie, deren Höhe von der Anzahl der Fermionen in dem betrachteten System abhängt und als Fermi-Kante, Fermi-Grenze oder Fermi-Energie Ef bezeichnet wird. Ganz wichtig ist hierbei, dass die Fermi-Verteilung nur eine Wahrscheinlichkeit angibt, mit der ein Zustand besetzt wird. Ob der Zustand auch besetzt wird, hängt davon ab, ob ein entsprechender Zustand existiert. Bei einem Halbleiter existiert zur Fermi-Energie kein erlaubter Zustand, er kann nicht besetzt werden (verbotene Zone).
Für die Temperatur Null Kelvin (T = 0 K) gilt eine scharfe Grenze (siehe Abbildung rechts):
- Alle Zustände unter der Fermi-Energie Ef sind mit Fermionen besetzt, da für E < Ef gilt: W(E) = 1, d. h. Wahrscheinlichkeit, ein Fermion anzutreffen ist Eins.
- Zustände oberhalb der Fermi-Energie sind nicht von Fermionen besetzt, da für E > Ef gilt: W(E) = 0, die Wahrscheinlichkeit ein Fermion anzutreffen also Null ist.
- Das elektrochemische Potenzial des Systems entspricht der Fermi-Energie.
Die Temperatur, bei der die thermische Energie kBT der Fermi-Energie entspräche, wird als Fermi-Temperatur Tf bezeichnet. Diese Begriffsbildung dient nur dem Charakterisieren einer Temperaturskala (s. u.) und hat nichts mit der realen Temperatur der Fermionen zu tun. Für Metalle liegt Tf über 10000 K.
Fermi-Verteilung bei endlichen und sehr hohen Temperaturen
_svg.png) Abgerundete Kurve: Fermi-Verteilung für T=300 K und T=1200 K (das ist noch deutlich unterhalb der Temperatur Tf:= Ef/kB, mit der Boltzmannkonstante kB; die Temperatur Tf entspricht einigen 10.000 Kelvin; hier sollte man trotzdem die Fermi-Energie Ef eigentlich durch das Chemische Potenzial μ ersetzen; im Rahmen der Messgenauigkeit sind sie jedoch identisch, weil die relative Abweichung für kBT << Ef enorm klein ist, nämlich bis auf einen Faktor der Größenordnung −1 (freie Elektronen) oder +1 (Nickel), identisch mit (kBT/Ef)2. Die gestrichelte Kurve soll nur zeigen, dass μ(1/2) genau 0,5 ist.).
Abgerundete Kurve: Fermi-Verteilung für T=300 K und T=1200 K (das ist noch deutlich unterhalb der Temperatur Tf:= Ef/kB, mit der Boltzmannkonstante kB; die Temperatur Tf entspricht einigen 10.000 Kelvin; hier sollte man trotzdem die Fermi-Energie Ef eigentlich durch das Chemische Potenzial μ ersetzen; im Rahmen der Messgenauigkeit sind sie jedoch identisch, weil die relative Abweichung für kBT << Ef enorm klein ist, nämlich bis auf einen Faktor der Größenordnung −1 (freie Elektronen) oder +1 (Nickel), identisch mit (kBT/Ef)2. Die gestrichelte Kurve soll nur zeigen, dass μ(1/2) genau 0,5 ist.).Bei endlichen Temperaturen (T > 0 K), die klein gegenüber der sog. Fermi-Temperatur Tf sind (es soll also gelten
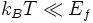 , mit der Boltzmann-Konstante kB) werden auch Zustände oberhalb der Fermi-Energie Ef mit Fermionen besetzt, dafür bleiben gleich viele Zustände unterhalb der Fermi-Energie leer. Die Verteilung der Energie wird durch die Fermi-Dirac-Statistik beschrieben, die bei T > 0 K an der „Fermi-Kante“ in einem Bereich der Breite ~ 2kBT aufgeweicht ist. Die Fermi-Verteilung lässt sich dabei im Bereich sehr hoher Energien,
, mit der Boltzmann-Konstante kB) werden auch Zustände oberhalb der Fermi-Energie Ef mit Fermionen besetzt, dafür bleiben gleich viele Zustände unterhalb der Fermi-Energie leer. Die Verteilung der Energie wird durch die Fermi-Dirac-Statistik beschrieben, die bei T > 0 K an der „Fermi-Kante“ in einem Bereich der Breite ~ 2kBT aufgeweicht ist. Die Fermi-Verteilung lässt sich dabei im Bereich sehr hoher Energien, 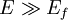 , ebenso wie die Bose-Einstein-Verteilung für Bosonen, durch die Boltzmann-Verteilung
, ebenso wie die Bose-Einstein-Verteilung für Bosonen, durch die Boltzmann-Verteilungnähern.
Ist die Temperatur sehr viel größer als die Fermi-Temperatur Tf = Ef/kB, so sind nunmehr alle Fermionen angeregt und die Boltzmann-Näherung gilt für den gesamten Energiebereich. In Metallen liegt die Fermi-Energie jedoch in der Größenordnung einiger Elektronenvolt entsprechend einer Fermi-Temperatur von einigen 10.000 K. Dies hat zur Folge, dass auch bei Zimmertemperatur der Einfluss der Temperatur vernachlässigbar ist bzw. nur störungstheoretisch berücksichtigt werden muss. In diesem Fall spricht man von einem entarteten Elektronengas.
In Metallen kann der Beitrag des heißen „Elektronengases“ für die Ermittlung der Wärmekapazität vernachlässigt werden, solange die Temperatur weit unter der Fermi-Temperatur Tf bleibt.
Bedeutung
In Festkörpern kann die Fermi-Verteilung mit Experimenten, die die elektronische Besetzungsdichte messen, sehr gut beobachtet und ausgewertet werden. Mit solchen Studien lässt sich das Auflösungsvermögen einer Messapparatur bestimmen, indem man den Verlauf der Fermi-Verteilung bei einer bestimmten Temperatur misst und mit der Theorie vergleicht.
Genauso verringert die Fermi-Verteilung das Auflösungsvermögen bei endlichen Temperaturen. Unter der Annahme, dass sich die Fermi-Verteilung bei einer bestimmten Temperatur näherungsweise als Faltung einer Stufenfunktion und einer Gauß-Verteilung einer bestimmten Breite beschreiben lässt, entsprechen 1 K etwa 0,34 meV. Das Auflösungsvermögen einer Apparatur, die Effekte misst, bei denen die Verteilung der Elektronen in unmittelbarer Umgebung der Fermi-Energie eine Rolle spielt, ist bei Raumtemperatur somit auf 100 meV begrenzt.
Literatur
- Ellen Ivers-Tiffée, Waldemar von Münch: Werkstoffe der Elektrotechnik. 10. Auflage. Vieweg+Teubner, 2007, ISBN 978-3-8351-0052-7.
- Michael Reisch: Halbleiter-Bauelemente. 2. Auflage. Springer-Verlag, Berlin 2004, ISBN 3-540-21384-8.
Wikimedia Foundation.

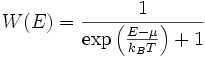
_svg.png)