Formelsammlung Elektrostatik

Ladung / Verschiebungsfluss

Einheit

Q bzw. q = Ψ. Einheit: [Q] = C = As (Coulomb = Ampere Sekunde)

Ladungserhaltung

$Q_{\rm tot}\,=\,\sum_{i} Q_i\,=\,\int\limits_{V}{ q_i \,\cdot\,\mathrm{d}V}$

$Q_{\rm tot}\,$: Gesamtladung im abgeschlossenen System

$Q_{i}\,/\,q_i$: Einzelladungen

$V\,,\,\mathrm{d}V$: Volumen , infinitesimales Volumenelement

Anziehungskraft zweier Punktladungen

skalar:

$F\,=\,\frac{1}{4\pi\varepsilon }\,\cdot\,\frac{Q_1Q_2}{r^2} \qquad \mathrm{mit} \quad \varepsilon = \varepsilon_0\varepsilon_{\rm r}$

vektoriell:

$\vec{F}\,=\,\frac{1}{4\pi\varepsilon }\,\cdot\,\frac{Q_1Q_2}{r^2}\,\cdot\,\frac{\vec{r}}{r} \qquad \mathrm{mit} \quad \varepsilon = \varepsilon_0\varepsilon_{\rm r}$

$\varepsilon\,$: Permittivität (Dielektrizitätszahl)

$\varepsilon_0\,$: elektrische Feldkonstante $=\,8{,}85418782\dots\cdot10^{-12}\,\frac{\rm As}{\rm Vm}$

$\varepsilon_{\rm r}\,$: relative Permittivität (relative Dielektrizitätszahl)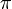

$\pi\,$: (Pi) Kreiszahl $=\,3{,}14159265\dots$

$Q_1\,,\, Q_2$: Ladungen

$\vec{r}\,$: Abstandsvektor der Ladungen

$r\,=\,|\vec{r}|\,$: Abstand der Ladungen

Verschiebungsfluss

skalar:

$\Psi\,=\,Q\,=\,\sum{\varepsilon\,\cdot E_N\,\cdot\,\Delta A} \qquad \textrm{mit} \quad \varepsilon = \varepsilon_0\varepsilon_r$

wenn homogen:

$\Psi\,=\,Q\,=\,\int\limits_{A}{ D\,\cdot\,\mathrm{d}A}$

vektoriell:

$\Psi\,=\,Q\,=\,\int\limits_{A}{\varepsilon\,\cdot\vec{E}\,\cdot\,\vec{\mathrm{d}A}} \quad \mathrm{mit} \quad \varepsilon = \varepsilon_0\varepsilon_{\rm r}$

$\Psi\,=\,Q\,=\,\int\limits_{A}{\vec{D}\,\cdot\,\vec{\mathrm{d}A}}$

geschlossene Fläche:

$\Psi\,=\,\sum_{A}{Q_e}$

Q_e: eingeschlossene Ladung

$\varepsilon\,$: Permittivität (Dielektrizitätszahl)

$\varepsilon_0\,$: elektrische Feldkonstante $=\,8{,}85418782\dots\cdot10^{-12}\,\frac{\rm As}{\rm Vm}$

$\varepsilon_{\rm r}\,$: relative Permittivität (relative Dielektrizitätszahl)

$E_N\,=\,|\vec{E}|\cdot\,\cos(\varphi)\,$: Normalkomponente

nach oben

elektrische Feldstärke

die elektrische Feldstärke (E-Feld) und deren Einheit

Die elektrische Feldstärke ist eine vektorielle Größe; sie hat somit ein Betrag und eine Richtung.

$\vec{E} \qquad {\rm Einheit:}\,\frac{\rm V}{\rm m}\, {\rm bzw.} \,\frac{\rm N}{\rm C}$

Die Einheiten veranschaulichen die einfachste Berechnungen des E-Feldes:

$\vec{E}\,=\,\frac{\vec{F}}{q}\,=\,\frac{\mathrm{d}U}{\vec{\mathrm{d}l}}$

Feldstärke im Potenzialfeld:

$\vec E = - \operatorname{grad}(\varphi)$

E-Feld einer Punktladung

skalar:

$E\,=\,\frac{1}{4\pi\varepsilon }\,\cdot\,\frac{Q}{r^2} \quad {\rm mit}\quad \varepsilon = \varepsilon_0\varepsilon_{\rm r}$

vektoriell:

$\vec{E}\,=\,\frac{1}{4\pi\varepsilon }\,\cdot\,\frac{Q}{r^2}\,\cdot\,\frac{\vec{r}}{r} \quad {\rm mit}\quad \varepsilon = \varepsilon_0\varepsilon_{\rm r}$

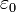$\varepsilon_0$: Elektrische Feldkonstante $=\,8{,}85418782\dots\cdot10^{-12}\,\frac{\rm As}{\rm Vm}$

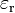$\varepsilon_{\rm r}$: Dielektrizitätszahl

E-Feld eines geladenen Leiters

äußeres Feld:

skalar:

$E\,=\,\frac{Q}{2\pi\varepsilon lr}\,=\,\frac{\rho}{2\pi\varepsilon r} \quad {\rm mit} \quad \rho=\frac Ql$

vektoriell:

$\vec{E}(P)\,=\,\frac{Q}{2\pi\varepsilon l(\vec{p}\times\vec{e_l})^2}\cdot (\vec{e_l}\times(\vec{p}\times\vec{e_l}))\,=\,\frac{\rho}{2\pi\varepsilon (\vec{p}\times\vec{e_l})^2}\cdot (\vec{e_l}\times(\vec{p}\times\vec{e_l})) \quad {\rm mit} \quad \vec{e_l}=\frac{\vec l}{|\vec l|},\quad \vec{p}=\vec{OP}$

inneres Feld:

Für eine Statische Ladungsverteilung muss die Summe aller Kräfte auf jede Ladung 0 sein. Da Ladungen im inneren eines Leiters frei beweglich sind gilt, darf es kein Feld geben. Diesem würde jede Ladung folgen, bis auftretende Ladungsverteilungen das Ursprungsfeld kompensieren. Das heißt, dass es keine Potentialdifferenz gibt:

ΔU = 0.

$U(\vec{r})=const.$ erfüllt diese Bedingung. Wonach das Feld 0 sein muss:

$\vec{E}(\vec{r})=-\nabla U(\vec{r})=0$

Nach dem Eindeutigkeitssatz, ist dies die richtige Lösung.

nach oben

Spannung / Potential

die Spannung / das Potential und deren Einheit

$U \qquad {\rm Einheit}\,{\rm ist}\,{\rm Volt:}\,{\rm V} = \frac{\rm J}{\rm C}$

$\varphi \qquad {\rm Einheit:}\,{\rm V}$

Spannung zwischen zwei Punkten im E-Feld

$U_{AB}\,=\,\frac{W_{AB}}{q}$

$U_{AB}\,=\,\int\limits_{A}^{B}{\vec{E}\cdot\vec{\mathrm{d}s}}$

im homogenen Feld:

$U_{AB}\,=\,\vec{E}\cdot\vec{s}$

Potential im E-Feld

$\varphi_{A}\,=\,U_{AZ}\,=\,-\int\limits_{Z}^{A}{\vec{E}\cdot\vec{\mathrm{d}s}}$

Z: Bezugspunkt; $\varphi_{Z}\,=\,0$

nach oben

Kapazität

die Kapazität und deren Einheit

die Kapazität ist ein Maß für die Speicherfähigkeit eines Kondensators:

$C \qquad {\rm Einheit\;ist\; Farad:}\, \mathrm{F = \frac C V}$

Die Einheit veranschaulicht die einfachste Berechnung der Kapazität:

$C\,=\,\frac{Q}{U}\,=\,\frac{\mathrm{d}U}{\vec{\mathrm{d}l}}$

Kapazität eines Plattenkondensators

$C\,=\,\varepsilon\frac{A}{d} \quad {\rm mit}\quad \varepsilon = \varepsilon_0\varepsilon_{\rm r}$

$\varepsilon$: Permittivität (Dielektrizitätszahl)

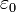$\varepsilon_0$: elektrische Feldkonstante $=\,8{,}85418782\dots\cdot10^{-12}\,\frac{\rm As}{\rm Vm}$

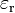$\varepsilon_{\rm r}$: relative Permittivität (relative Dielektrizitätszahl)

Kapazität eines Zylinderkondensators

könnte z.B. ein Koax-Kabel sein

$C\,=\,\frac{2\pi\varepsilon l}{\ln{\frac{r_{\rm a}}{r_{\rm i}}}} \quad {\rm mit}\quad \varepsilon = \varepsilon_0\varepsilon_{\rm r}$

r_a: Außenradius

r_i: Innenradius

l: Zylinderlänge

Kapazität einer freistehenden Kugel

$C\,=\,4\pi\varepsilon r \quad {\rm mit}\quad \varepsilon = \varepsilon_0\varepsilon_{\rm r}$

r: Kugelradius

Kapazität eines Kugelkondensators

$C\,=\,\frac{4\pi\varepsilon}{\left({\frac{1}{r_{\rm i}}-\frac{1}{r_{\rm a}}}\right)} \quad {\rm mit}\quad \varepsilon = \varepsilon_0\varepsilon_{\rm r}$

r_a: äußerer Kugelradius

r_i: innerer Kugelradius

nach oben