- Frechet-Metrik
-
Fréchet-Metrik (nach Maurice René Fréchet) ist ein Begriff aus der Funktionalanalysis. Sie stellt eine Verbindung zwischen Metrik und Norm her.
Inhaltsverzeichnis
Definition
Sei X ein beliebiger Vektorraum. Eine Fréchet-Metrik ist eine Abbildung
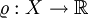 , die für
, die für 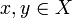 folgende Bedingungen erfüllt:
folgende Bedingungen erfüllt:-
-
- (1)
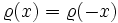
- (2)
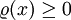 , wobei
, wobei 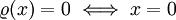
- (3)
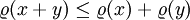
- (1)
-
Das heißt,
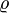 ist symmetrisch, nichtnegativ und genügt der Dreiecksungleichung.
ist symmetrisch, nichtnegativ und genügt der Dreiecksungleichung.Anwendungen
- Durch eine Fréchet-Metrik kann in einem Vektorraum eine Metrik definiert werden vermöge
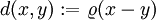 . Dass die so definierte Abbildung eine Metrik ist, folgt direkt aus der Definition der Fréchet-Metrik.
. Dass die so definierte Abbildung eine Metrik ist, folgt direkt aus der Definition der Fréchet-Metrik. - Umgekehrt gilt: Jede Metrik d auf einem Vektorraum, die translationsinvariant ist, d.h. d(x + c,y + c) = d(x,y), entsteht durch genau eine solche Fréchet-Metrik.
- Jede Norm
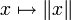 auf X ist eine Fréchet-Metrik, denn
auf X ist eine Fréchet-Metrik, denn  erfüllt offensichtlich die Bedingungen (2) und (3). Die Gültigkeit von (1) folgt aus der Homogenität von Normen. Die Umkehrung gilt jedoch nicht: Beispielsweise ist für
erfüllt offensichtlich die Bedingungen (2) und (3). Die Gültigkeit von (1) folgt aus der Homogenität von Normen. Die Umkehrung gilt jedoch nicht: Beispielsweise ist für 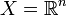 die Fréchet-Metrik
die Fréchet-Metrik 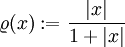 keine Norm, da sie nicht homogen ist.
keine Norm, da sie nicht homogen ist. - Ein topologischer Vektorraum besitzt genau dann eine Fréchet-Metrik, die seine Topologie erzeugt, wenn er erstabzählbar ist.
- Wenn ein (reeller oder komplexer) Vektorraum mit Fréchet-Metrik die zusätzlichen Eigenschaften hat, dass er vollständig ist und dass die Topologie dieses Vektorraums lokalkonvex ist, dann handelt es sich um einen Fréchet-Raum.
Literatur
- H. W. Alt: "Lineare Funktionalanalysis", 4. Aufl., Berlin, Springer, 2002, ISBN 3-540-43947-1.
Siehe auch
-
Wikimedia Foundation.
