- Lokalkonvex
-
Lokalkonvexer Vektorraum berührt die Spezialgebiete
ist Spezialfall von
umfasst als Spezialfälle
Die lokale Konvexität ist eine Eigenschaft eines topologischen Vektorraumes. Ein lokal konvexer Raum kann als eine Verallgemeinerung eines normierten Vektorraumes bzw. eines normierbaren Vektorraumes betrachtet werden. Lokalkonvexe Räume werden in der Funktionalanalysis untersucht.
Inhaltsverzeichnis
Geometrische Definition
Ein topologischer Vektorraum V heißt lokal konvex, wenn jede Nullumgebung U eine offene Teilmenge T enthält mit den folgenden drei Eigenschaften:
- T ist konvex.
- T ist absorbierend.
- T ist ausgewogen.
Eine Teilmenge T eines reellen oder komplexen Vektorraumes heißt absorbierend, wenn es zu jedem Vektor x in V eine echt positive reelle Zahl r gibt, so dass rx ein Element von T ist.
Eine Teilmenge T eines reellen oder komplexen Vektorraumes heißt ausgewogen, wenn zu jedem Vektor x in T und jeder Zahl r mit |r|<1 der Vektor rx ebenfalls in T liegt. (Die Strecke von -x nach x liegt in T.) Aufgrund der geometrischen Bedeutung dieser Definition werden solche Mengen manchmal auch kreisförmig genannt.
Eine ausgewogene und konvexe Menge heißt absolutkonvexe Menge.
Es stellt sich heraus, dass die zweite und dritte Bedingung in gewisser Weise überflüssig sind. Es gibt genau dann eine Nullumgebungsbasis aus konvexen, absorbierenden und ausgewogenen Mengen, wenn es eine Nullumgebungsbasis aus konvexen Mengen gibt. (Diese beiden Umgebungsbasen müssen natürlich nicht übereinstimmen, aber die Existenz der einen impliziert die Existenz der anderen)
Definition durch Halbnormen
Lokalkonvexe Räume lassen sich auch durch Halbnormen-Systeme charakterisieren: Ein topologischer Vektorraum V heißt lokal konvex, wenn seine Topologie durch eine Familie
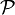 von Halbnormen definiert ist. Die Kugeln bezüglich der Halbnormen
von Halbnormen definiert ist. Die Kugeln bezüglich der Halbnormen 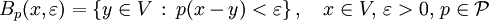 bilden dabei eine Subbasis der Topologie.
bilden dabei eine Subbasis der Topologie.Beispiele
- Direkte Limites von Banachräumen wie
 mit der Familie der Halbnormen
mit der Familie der Halbnormen ![p_k(f)= \max_{x \in [-k,k]} |f(x)|](/pictures/dewiki/51/367483fc599cc3b93441e29653771b13.png) .
. - Alle topologischen Vektorräume mit der schwachen Topologie.
- Alle Banachräume sind lokal konvex, wobei die Familie
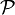 nur die (echte) Norm enthält.
nur die (echte) Norm enthält. - Banachräume mit schwacher Topologie sowie Dualräume von Banachräumen mit der schwach-*-Topologie sind lokal konvex, wobei die Familie
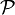 hier durch die Funktionale aus dem Dual- respektive Prädualraum mittels
hier durch die Funktionale aus dem Dual- respektive Prädualraum mittels 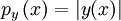 (y ist das Funktional) erzeugt werden.
(y ist das Funktional) erzeugt werden. - Projektive Limites von Banachräumen sind lokal konvex. Die Familie
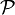 ist durch die Normen der Banachräume, deren Limes gebildet wird, gegeben. Konkretes Beispiel:
ist durch die Normen der Banachräume, deren Limes gebildet wird, gegeben. Konkretes Beispiel:![\mathcal{C}^\infty([0,1])](/pictures/dewiki/48/0806a56d4a339629a1b702d68c65192c.png) mit der Familie der Normen
mit der Familie der Normen ![p_k(f)= \sum_{i\leq k} \max_{x \in [0,1]} |f^{(i)}(x)|.](/pictures/dewiki/57/9c78c8abdb8f677e71859911fc0c9aec.png) Obwohl die Familie aus echten Normen besteht, ist der Raum kein Banachraum!
Obwohl die Familie aus echten Normen besteht, ist der Raum kein Banachraum! - Der Raum
![L^p\left([0,1]\right)](/pictures/dewiki/50/293fe15e5a2dc78fd1c0a15e1ddd93e1.png) (siehe Lp-Raum) ist für 0 < p < 1 ein topologischer (sogar metrisierbarer) Vektorraum, der nicht lokalkonvex ist.
(siehe Lp-Raum) ist für 0 < p < 1 ein topologischer (sogar metrisierbarer) Vektorraum, der nicht lokalkonvex ist.
Eigenschaften
Erfüllt die Halbnormenmenge aus obiger Definition
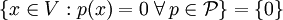 , so ist der Raum ein Hausdorff-Raum. Viele Autoren betrachten nur Hausdorff'sche lokalkonvexe Räume.
, so ist der Raum ein Hausdorff-Raum. Viele Autoren betrachten nur Hausdorff'sche lokalkonvexe Räume.Hausdorffsche, lokal konvexe Räume haben genügend viele stetige, lineare Funktionale, um Punkte zu trennen, d.h. für alle
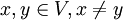 gibt es ein stetiges, lineares Funktional f mit
gibt es ein stetiges, lineares Funktional f mit 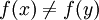 . Das zeigt sich in der Gültigkeit wichtiger Sätze wie
. Das zeigt sich in der Gültigkeit wichtiger Sätze wie- Der Satz von Hahn-Banach
- Der Trennungssatz
- Der Satz von Krein-Milman
Die stetigen, linearen Funktionale auf einem topologischen Vektorraum V trennen genau dann die Punkte, wenn es eine gröbere Topologie auf V gibt, die V zu einem hausdorffschen, lokalkonvexen Raum macht. Die Untersuchung lokalkonvexer Räume mittels stetiger, linearer Funktionale führt zu einer sehr weitreichenden Theorie, die für allgemeine topologische Vektorräume so nicht möglich ist. Es gibt topologische Vektorräume, die außer dem Nullfunktional kein weiteres stetiges, lineares Funktional besitzen.
Verallgemeinerungen
Spezielle lokalkonvexe Räume
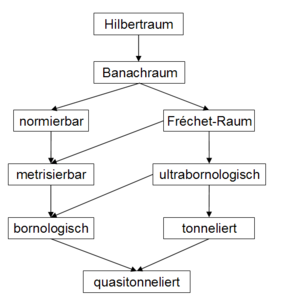
Viele Klassen lokalkonvexer Räume zeichnen sich durch die Gültigkeit bestimmter Sätze, die aus der Theorie der Banachräume oder normierten Räume bekannt sind, aus. So sind z.B. die tonnelierten Räume genau diejenigen lokalkonvexen Räume, in denen der Satz von Banach-Steinhaus noch gilt. Diese Sätze können in den entsprechenden Raumklassen in 'Reinkultur' untersucht werden, ihre Tragweite wird deutlich. Die bekanntesten dieser Raumklassen sind:
- bornologischer Raum (ultrabornologischer Raum)
- tonnelierter Raum (quasitonnelierter Raum)
- metrisierbarer lokalkonvexer Raum
- Fréchet-Raum
- normierter Vektorraum
- Banachraum
- Hilbertraum
Räume differenzierbarer oder holomorpher Funktionen tragen natürliche lokalkonvexe Topologien, deren Eigenschaften zu weiteren Raumklassen Anlass geben. Die wichtigsten dieser Raumklassen, die zu einem tieferen Verständnis der lokalkonvexen Theorie führen, sind etwa
- Nuklearer Raum
- Montel-Raum
- Schwartz-Raum
- (DF)-Raum (gDF-Raum)
- quasinormierbarer Raum
- (LF)-Raum (LB-Raum)
- Raum mit Gewebe
Literatur
- G. Köthe, Topological Vector Spaces I (2.te Auflage), Springer, 1983, ISBN 3-540-04509-0
- G. Köthe, Topological Vector Spaces II, Springer, 1979, ISBN 3-540-90400-X
- K. Floret, J. Wloka: Einführung in die Theorie der lokalkonvexen Räume, Lecture Notes in Mathematics 56, 1968
- H. H. Schaefer: Topological Vector Spaces, Springer, 1971 ISBN 0-387-98726-6
- H. Jarchow: Locally Convex Spaces, Teubner, Stuttgart 1981 ISBN 3-519-02224-9
- R. Meise, D. Vogt: Einführung in die Funktionalanalysis, Vieweg, 1992 ISBN 3-528-07262-8
Wikimedia Foundation.