Frei abelsche Gruppe

In der Mathematik ist eine freie abelsche Gruppe eine abelsche Gruppe, die eine "Basis" hat, so dass jedes Element der Gruppe auf genau eine Weise als endliche Linearkombination der Basis mit ganzzahligen Koeffizienten geschrieben werden kann.

Im Gegensatz zu Vektorräumen hat nicht jede abelsche Gruppe eine Basis, deshalb gibt es diesen spezielleren Begriff.

Beachte: Eine freie abelsche Gruppe ist nicht dasselbe wie eine freie Gruppe, die abelsch ist; in der Tat sind die meisten freien Gruppen nicht abelsch, und die meisten freien abelschen Gruppen sind keine freien Gruppen. Es gibt deshalb auch die Bezeichnung frei abelsche Gruppe, in der frei abelsch als ein einzelnes Attribut aufgefasst wird.

Formale Definition

Sei F eine abelsche Gruppe und B eine Teilmenge von F. Dann heißt F freie abelsche Gruppe mit Basis B, wenn gilt:

B ist Z-linear unabhängig, d.h. das neutrale Element kann nur auf eine einzige Weise als Z-Linearkombination von B dargestellt werden,

jedes Element von F ist als endliche Z-Linearkombination von B darstellbar.

Beispiele

Die Gruppen (Z, +) und (Z×Z, +) (mit komponentenweiser Addition) sind freie abelsche Gruppen mit der Basis {1} bzw. {(1,0), (0,1)}.

Endliche abelsche Gruppen (außer der einelementigen Gruppe) können keine freien abelschen Gruppen sein, da das neutrale Element auf verschiedene Weisen darstellbar ist.

Die Menge der Folgen ganzer Zahlen, die nur endlich viele von 0 verschiedene Komponenten haben, ist mit der komponentenweisen Addition eine freie abelsche Gruppe; eine Basis bilden die kanonischen Einheitsvektoren (0, ..., 0, 1, 0, ...).

Konstruktion

Für jede Menge B gibt es immer eine freie abelsche Gruppe mit Basis B. Diese Gruppe ist im folgenden Sinne eindeutig: Sind F₁ und F₂ zwei freie abelsche Gruppen mit Basis B, dann sind sie isomorph, und es gibt genau einen Isomorphismus 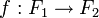$f:F_1 \to F_2$ zwischen ihnen, der f(s) = s für alle s aus B erfüllt. Diese Eindeutigkeit erlaubt es, von der freien abelschen Gruppe mit Basis B zu sprechen.

Die freie abelsche Gruppe mit Basis B kann wie folgt konstruiert werden: Wir betrachten die Menge F(B) aller Funktionen von B in die ganzen Zahlen, die nur an endlich vielen Stellen von 0 verschiedene Werte annehmen. Diese Menge ist eine abelsche Gruppe mit der komponentenweisen Addition. Wenn wir nun jedes Element b∈B mit seiner charakteristischen Funktion identifizieren (also mit jener auf B definierten Funktion, die an der Stelle b den Wert 1 annimmt und sonst den Wert 0), so ist F(B) frei abelsch mit Basis B.

Universelle Eigenschaft

Die freie abelsche Gruppe mit Basis B ist charakterisiert durch folgende universelle Eigenschaft: Ist A eine abelsche Gruppe und f: B → A eine beliebige Funktion, dann gibt es genau einen Gruppenhomomorphismus 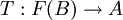$T:F(B) \to A$, der f fortsetzt.

Eigenschaften

Jede endlich erzeugte freie abelsche Gruppe ist isomorph zur Gruppe Zⁿ für eine natürliche Zahl n. Diese Zahl n ist eindeutig bestimmt und heißt der Rang der freien abelschen Gruppe.

Im allgemeinen haben alle Basen einer freien abelschen Gruppe die gleiche Mächtigkeit, die man Rang nennt. Dieser Rang kann benutzt werden, um allen anderen abelschen Gruppen einen Rang zuzuweisen, siehe Rang einer abelschen Gruppe.

Jede Untergruppe einer freien abelschen Gruppe ist frei abelsch.

Freie abelsche Gruppen sind spezielle freie Moduln, da jede abelsche Gruppe als Z-Modul aufgefasst werden kann.

Jede freie abelsche Gruppe ist torsionsfrei, aber die torsionsfreie abelsche Gruppe (Q, +) ist nicht frei abelsch.

Literatur

Gisbert Wüstholz: Algebra. Vieweg 2004. ISBN 3-528-07291-1