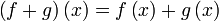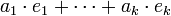Kommutative Gruppe

Abelsche Gruppe (=kommutative Gruppe) (Axiome EANIK)

berührt die Spezialgebiete

Mathematik Abstrakte Algebra Gruppentheorie

ist Spezialfall von

Magma (Axiom E) Halbgruppe (EA) Monoid (EAN) Gruppe (EANI)

umfasst als Spezialfälle

endliche Abelsche Gruppen zyklische Gruppen Ring Körper Vektorraum

In der abstrakten Algebra ist eine abelsche Gruppe eine Gruppe (G, * ), für die das Kommutativgesetz

a * b = b * a für alle $a, b \in G$

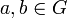
gilt. Sie ist benannt nach dem norwegischen Mathematiker Niels Henrik Abel.

Ist eine Gruppe abelsch, dann schreibt man ihre Verknüpfung meist additiv (Operator „+“; 0 als das neutrale Element oder Nullelement; −a als das Inverse oder Negative von a) oder multiplikativ (Operator „·“; 1 als das neutrale Element oder Einselement; a ^{− 1} als das Inverse oder Kehrwert von a).

Beispiele

Jede zyklische Gruppe ist abelsch; Beispiele sind die additive Gruppe 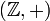$(\Bbb Z, +)$ der ganzen Zahlen oder der Restklassenring 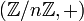$(\Bbb Z/n\Bbb Z, +)$ mit der Addition.

Die reellen Zahlen bilden eine abelsche Gruppe mit der Addition; ohne die Null bilden sie eine abelsche Gruppe mit der Multiplikation.

Allgemeiner liefert jeder Körper 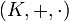$(K, +, \cdot)$ in derselben Weise zwei abelsche Gruppen (K, + ) und $(K\setminus\{0\}, \cdot)$.

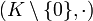Ein weiteres Beispiel ist die Faktorgruppe 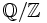$\Bbb Q/\Bbb Z$, die isomorph zur (multiplikativen) Gruppe der komplexen Einheitswurzeln ist. Die Faktorgruppe 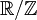$\R/\Bbb Z$ ist isomorph zur Gruppe aller komplexen Zahlen mit Betrag 1.

Eigenschaften

Für eine (kleine) endliche Gruppe erkennt man leicht, ob sie abelsch ist:

Genau dann, wenn eine Gruppe abelsch ist, ist ihre Gruppentafel symmetrisch zur Hauptdiagonalen, die von links oben nach rechts unten führt.

Ist n eine natürliche Zahl und x ein Element der abelschen Gruppe G, dann kann man nx definieren als die Summe 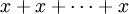$x+x+\cdots+x$ mit genau n Summanden, 0x als 0 (das neutrale Element der Gruppe) und (−n)x als −(nx). Auf diese Weise wird G zu einem Modul über dem Ring Z. Da jeder Z-Modul eine abelsche Gruppe ist, kann man also die Z-Moduln mit den abelschen Gruppen identifizieren. Theoreme über abelsche Gruppen können so oft verallgemeinert werden zu Sätzen für Moduln über Hauptidealringen. Ein Beispiel ist die Klassifikation endlich erzeugter abelscher Gruppen (siehe unten).

Jede Untergruppe einer abelschen Gruppe ist ein Normalteiler, also kann man zu jeder Untergruppe eine Faktorgruppe erzeugen. Untergruppen, Faktorgruppen, Produkte und direkte Summen abelscher Gruppen sind wieder abelsch.

Sind 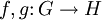$f, g\colon G \to H$ zwei Gruppenhomomorphismen zwischen abelschen Gruppen, dann ist ihre Summe f + g, definiert durch

$\left(f+g\right)\left(x\right) = f\left(x\right)+g\left(x\right)$

ebenfalls ein Homomorphismus. (Das gilt nicht, wenn H nicht abelsch ist.) Die Menge Hom(G, H) aller Gruppenhomomorphismen wird mit dieser Addition selbst zu einer abelschen Gruppe.

Die abelschen Gruppen mit ihren Homomorphismen bilden eine Kategorie. Diese ist der Prototyp einer abelschen Kategorie.

Viele abelsche Gruppen haben eine natürliche Topologie, durch die sie zu topologischen Gruppen werden.

Zusätzliche Attribute

• Eine abelsche Gruppe ist genau dann endlich erzeugt, wenn es eine endliche Menge 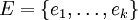$E = \{e_1, \ldots, e_k\}$ gibt, so dass sich jedes Element in der Form

$a_1\cdot e_1+ \cdots +a_k \cdot e_k$

mit ganzen Zahlen 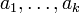$a_1, \ldots, a_k$ schreiben lässt. Insbesondere ist jede endliche abelsche Gruppen endlich erzeugt.

• Die Eigenschaften frei und projektiv sind äquivalent, ebenso torsionsfrei und flach.

Strukturtheorie

• Vollständig klassifiziert sind die endlich erzeugten abelschen Gruppen. Sie sind nämlich direkte Summen endlich vieler zyklischer Gruppen, und diese sind bis auf die Reihenfolge eindeutig bestimmt.
• Für beliebige abelsche Gruppen kann man analog zum Begriff der Dimension eines Vektorraums jeder abelschen Gruppe ihren Rang zuordnen. Er ist definiert als die größte Mächtigkeit einer $\mathbb{Z}$-linear unabhängigen Teilmenge. Die ganzen Zahlen und die rationalen Zahlen $\mathbb{Q}$ haben Rang 1, so wie jede Untergruppe von $\mathbb{Q}$. Die abelschen Gruppen vom Rang 1 sind gut verstanden, dagegen sind für höhere Ränge noch viele Fragen offen. Abelsche Gruppen mit unendlichem Rang können extrem komplex sein und ihre offenen Fragen sind oft eng verbunden mit Fragen der Mengenlehre.

Siehe auch

• Zentralisator
• Hierarchie mathematischer Strukturen