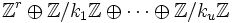Klassifikation endlich erzeugter abelscher Gruppen

In der abstrakten Algebra wird eine abelsche Gruppe (G,+) als endlich erzeugt bezeichnet, wenn es endlich viele Elemente x₁,...,x_s in G gibt, so dass jedes x aus G in der Form

x = n₁x₁ + n₂x₂ + ... + n_sx_s geschrieben werden kann, wobei

n₁,...,n_s ganze Zahlen sind. Wir sagen auch {x₁,...,x_s} sind die Erzeuger von G oder x₁,...,x_s erzeugen G.

Offensichtlich ist jede endliche abelsche Gruppe endlich erzeugt. Endlich erzeugte abelsche Gruppen sind von eher simpler Natur und können auf einfache Weise klassifiziert werden, wie weiter unten gezeigt wird.

Beispiele

• Die ganzen Zahlen (Z,+) sind eine endlich erzeugte Gruppe mit 1 als Erzeuger.
• Die ganze Zahlen modulo n, Z_n, bilden mit der Addition eine endlich erzeugte abelsche Gruppe.
• Jede direkte Summe von endlich vielen endlich erzeugten abelschen Gruppen ist wieder eine endlich erzeugte abelsche Gruppe.

Die Gruppe (Q,+) der rationalen Zahlen ist nicht endlich erzeugt: Zu x₁,...,x_s wähle man eine natürliche Zahl w, die teilerfremd zu allen Nennern ist; 1/w wird dann nicht erzeugt von x₁,...,x_s.

Klassifikation

Der Hauptsatz über endlich erzeugte abelsche Gruppen besagt, dass jede endlich erzeugte abelsche Gruppe G isomorph zu einer direkten Summe von unendlichen zyklischen Gruppen und zyklischen Gruppen, deren Ordnung die Potenz einer Primzahl ist, ist. Das heißt, jede solche Gruppe ist isomorph zu einer Gruppe der Form: 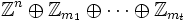$\mathbb{Z}^n \oplus \mathbb{Z}_{m_1} \oplus \cdots \oplus \mathbb{Z}_{m_t}$ mit n ≥ 0 und (nicht notwendig verschiedenen) Primpotenzen m₁,...,m_t. Die Zahlen n und m₁,...,m_t sind (bis auf die Reihenfolge) eindeutig durch G bestimmt; insbesondere ist G genau dann endlich, wenn n = 0.

Aufgrund der allgemeinen Tatsache, dass Z_m isomorph zu einer direkten Summe von Z_j und Z_k genau dann wenn j und k teilerfremd sind und m = jk, können wir jede abelsche Gruppe G als direkte Summe

$\mathbb Z^r\oplus \mathbb{Z}/k_1\mathbb Z \oplus \cdots \oplus \mathbb{Z}/k_u\mathbb Z$

schreiben, wobei die natürlichen Zahlen k_i > 1 mit der Eigenschaft 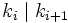$k_i \mid k_{i+1}$ für $i=1,\ldots,u-1$ eindeutig bestimmt sind.

Anders formuliert besagt der Hauptsatz, dass eine endlich erzeugte abelsche Gruppe die direkte Summe einer frei abelschen Gruppe von endlichem Rang und einer endlichen abelschen Gruppe ist. Die endliche abelsche Gruppe ist die Torsionsuntergruppe von G; die frei abelsche Gruppe ist im Allgemeinen nicht eindeutig bestimmt, sondern nur ihr Rang.

Man beachte, dass nicht jede abelsche Gruppe von endlichem Rang endlich erzeugt ist. Q zum Beispiel ist von Rang 1 aber nicht endlich erzeugt. Ein weiteres Beispiel ist die direkte Summe von unendlich vielen Kopien von Z₂, diese ist von Rang 0, aber auch nicht endlich erzeugt.

Ein Korollar zum Hauptsatz ist, dass die folgenden Eigenschaften für endlich erzeugte abelsche Gruppe äquivalent sind:

• frei
• projektiv
• torsionsfrei
• flach

Für nicht notwendig endlich erzeugte abelsche Gruppen wie beispielsweise Q sind lediglich die ersten beiden bzw. die letzten beiden äquivalent.

Jede Untergruppe und Faktorgruppe einer endlich erzeugten abelschen Gruppe ist wieder endlich erzeugt abelsch. Die endlich erzeugten abelschen Gruppen zusammen mit den Gruppenmorphismen bilden eine abelsche Kategorie.