- Gasschlag
-
Die Detonationswelle bezeichnet die durch eine Detonation (u.U. aber auch bei einer Deflagration) entstandene Stoßwelle innerhalb des gasförmigen, flüssigen oder festen umgebenden Mediums (ferner auch innerhalb des Sprengstoffes selbst), die sich vom Detonationsursprung ausgehend nach allen Seiten ausbreitet.
Inhaltsverzeichnis
Allgemeines
Abb. 1: Abnahme des Überdrucks und des dynamischen Drucks mit der EntfernungDie Detonationswelle bildet sich im Ergebnis einer Explosion in einem Medium, welches durch die rasche Expansion der gasförmigen Explosionsprodukte (oder auch einem erhitztem und dadurch sich ausdehnendem Teilvolumen des Mediums) schlagartig verdrängt wird.
Der Impuls wird von der einen Schicht zur nächsten Schicht durch die Stoßverdichtung weitergegeben, die einen Dichtesprung (auch: Front der Detonationswelle, Stoßfront) herbeiführt, der sich mit Überschallgeschwindigkeit ausbreitet. Geschieht dies innerhalb des Sprengmaterials, so führt dieser Stoß zur Zündung des von der Stoßfront getroffenen Materials, so dass die Stoßfront zugleich die Flammfront darstellt (Detonation). Bei einer Deflagration entsteht im Sprengmaterial zwar keine Stoßwelle; ist die Schallgeschwindigkeit des umgebenden Mediums jedoch deutlich geringer als die Geschwindigkeit, mit der sich die Explosionsprodukte ausdehnen, kann auch hier eine Detonationswelle entstehen.
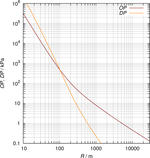
Die Detonationswelle wird durch eine räumliche und zeitliche Änderung des Druckes, der Dichte und der Geschwindigkeit der Front sowie der Moleküle des Mediums an den verschiedenen Punkten des Raumes oder durch die Verteilung dieser Größen im Raum zu fixierten Zeitpunkten gekennzeichnet. Beim Druck muss zwischen dem Überdruck infolge des Verdichtungsstoßes und dem durch die Teilchenbewegung bewirkten dynamischen Druck unterschieden werden. Im einfachsten Fall einer radialsymmetrischen Explosion sind sowohl der statische und dynamische Druck als auch die Laufzeit eine Funktion des Abstandes vom Ursprung (Abb. 1). In diesem Fall fällt der Druck streng monoton mit dem Abstand, während die Laufzeit ebenfalls streng monoton zunimmt. Beide Druck-Arten sind wesentliche Parameter, da sie auch den wichtigsten Einfluss der Sprengung auf das Sprenggut (Zertrümmern und Auseinandertreiben) ausüben.
Mit der Verringerung des maximalen Druckes wird auch die mechanische Wirkung der Detonationswelle schwächer. In großen Entfernungen verwandelt sich die Detonationswelle in eine Schallwelle oder in eine elastische Welle in einem festen Mittel, die sich mit einer konstanten, für das gegebene Mittel charakteristischen Geschwindigkeit ausbreitet.
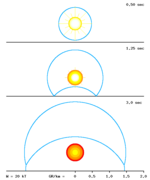
Abb. 2: Nichtlineare Reflexion der Druckwelle einer atomaren LuftexplosionEin wesentlich komplexeres Problem ist das Verhalten der Druckwelle unter Reflexion. Eine Explosion in der Nähe einer ebenen harten Fläche (z.B. Erdboden bei einer Luftexplosion, Abb. 2) führt zu einer Verstärkung der Druckwelle, die für unterschiedliche Abstände (Detonationshöhen) von der reflektierenden Fläche bei verschiedenen Druckwerten maximal wird. Das für Stoßwellen typische nichtlineare Verhalten bei Reflexionen wurde in den 1950er Jahren von den USA und der Sowjetunion in oberirdischen Kernwaffenversuchen ausführlich untersucht.
Ein Rechenmodell für atmosphärische Detonationswellen
Die frühere US-Behörde Defense Nuclear Agency (DNA) hat um 1984 ein Modell zur rechnerischen Abschätzung von Explosionsdruckwellen entwickelt, welches die Abhängigkeit der Überdruckspitze als Funktion der Distanz sowie der Detonationshöhe und der Sprengenergie liefert. Obgleich das Modell ursprünglich für Nuklearexplosionen entwickelt wurde, kann es über Skalierungsregeln auch auf nahezu beliebige andere Explosionstypen angewendet werden, sofern die Explosion von einer Punktquelle ausgeht und Inhomogenitäten im umgebenden Medium oder der reflektierenden Oberfläche vernachlässigbar sind. Das Modell, das in Gestalt eines DOS-Programms BLAST vorliegt, unterliegt keiner Geheimhaltung. Es baut im Wesentlichen auf der Rankine-Hugoniot-Gleichung sowie empirischer Fits auf der Basis von Kernwaffentest-Daten.
Ein Teil der zugrunde liegenden Formeln sind unter Formelsammlung Kernwaffenexplosion zu finden.
siehe auch
Literatur
- Kinney, G. F.; Graham, K. J.: “Explosive shocks in air“, Berlin/New York, Springer, 1985, ISBN 3-540-15147-8
Weblinks
Wikimedia Foundation.
