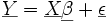Gauss-Markov-Annahmen

Die Artikel Satz von Gauß-Markow und Minimalvarianter linearer erwartungstreuer Schätzer überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen. Bitte entferne diesen Baustein erst nach vollständiger Abarbeitung der Redundanz. Chrisqwq 17:27, 24. Nov. 2006 (CET)

Der Satz von Gauß-Markow ist ein mathematischer Satz aus dem Bereich der Statistik. Er ist nach den Mathematikern Carl Friedrich Gauß und Andrei Andrejewitsch Markow benannt.

In Worten lautet dieser Satz: Der Kleinste-Quadrate-Schätzer ist ein minimalvarianter linearer erwartungstreuer Schätzer (BLUE – best linear unbiased estimator) in einem linearen Modell, wenn die zufälligen Fehler (nicht-erklärten Abweichungen):

• unkorreliert sind (keine Autokorrelation),
• einen Erwartungswert von Null haben und
• die gleiche Varianz haben (Homoskedastizität).

Mathematisch kann dies auf folgende Weise wiedergegeben werden: Voraussetzung ist, dass man ein Lineares Modell in der Form

$\underline Y = \underline X \underline \beta + \underline \epsilon$

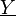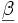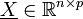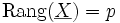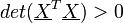vorliegen hat, wobei $\underline Y$ eine n-dimensionale und $\underline \beta$ eine p-dimensionale Zufallsvariable sei (siehe Regressionsanalyse). Hierbei nimmt man von der Datenmatrix $\underline X \in \mathbb{R}^{n \times p}$ an, dass sie vollen (Spalten-)Rang hat, das heißt es gilt $\mbox{Rang}(\underline{X})=p \;$ bzw. $det(\underline{X}^T \underline{X}) > 0$. Für den Erwartungswert der Fehler nimmt man an, dass 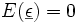$E(\underline{\epsilon})=0 \;$ ist. Ferner erwartet man für die Varianz der Fehler, dass 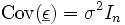$\mbox{Cov}(\underline{\epsilon})=\sigma^2 I_n$ gilt.

Damit erhält man:

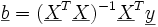1. $\underline b = (\underline {X}^T \underline X )^{-1} \underline {X}^T \underline y$ ist BLUE für $\underline \beta$.
2. $\mbox{Cov}(\underline{b})=\sigma^2 (\underline{X}^T \underline{X})^{-1}$
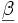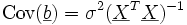
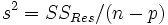3. $s^2 = SS_{Res} / (n-p) \;$ ist unverzerrter Schätzer für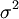 $\sigma^2 \;$

Wobei 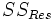$SS_{Res} \$ die Residual Sum of Squares bezeichnet.

Weblinks

• Carolo Friderico Gauss: Theoria combinationis observationum erroribus minimis obnoxiae (1821, 1823) Göttinger Digitalisierungszentrum
• A. A. Markoff: Wahrscheinlichkeitsrechnung (2. Auflage, 1912) Cornell University Library siehe insb. Kapitel 7
• Earliest Known Uses of Some of the Words of Mathematics (G) zur Herkunft des Namens
• Erklärungen zum Satz von Gauß-Markov von einem Mitarbeiter des Statistik-Lehrstuhls an der Universität Bonn Ausführungen
• Skriptum eines Mitarbeiters des Lehrstuhls für Statistik und Ökonometrie der Universität Erlangen