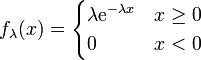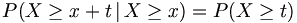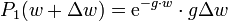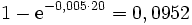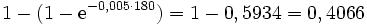Exponentialverteilt

Dichte der Exponentialverteilung mit verschiedenen Werten für λ

Die Exponentialverteilung ist eine stetige Wahrscheinlichkeitsverteilung über der Menge der positiven reellen Zahlen, die durch eine Exponentialfunktion gegeben ist. Sie wird als Modell vorrangig bei der Beantwortung der Frage nach der Dauer von zufälligen Zeitintervallen benutzt, wie z. B.

• Zeit zwischen zwei Anrufen
• Lebensdauer von Atomen beim radioaktiven Zerfall
• Lebensdauer von Bauteilen, Maschinen und Geräten, wenn Alterungserscheinungen nicht betrachtet werden müssen. (MTBF)
• als grobes Modell für kleine und mittlere Schäden in Hausrat, Kraftfahrzeug-Haftpflicht, Kasko in der Versicherungsmathematik

Oft ist die tatsächliche Verteilung keine Exponentialverteilung, jedoch ist die Exponentialverteilung einfach zu handhaben und wird zur Vereinfachung unterstellt. Sie ist anwendbar, wenn ein Prozess die poissonschen Annahmen erfüllt.

Definition

Eine stetige Zufallsvariable X genügt der Exponentialverteilung $\operatorname{Exp}(\lambda)$ mit dem Parameter λ, wenn sie die Wahrscheinlichkeitsdichte

$f_{\lambda}(x)= \begin{cases}\displaystyle \lambda{\rm e}^{-\lambda x} & x\geq 0 \\ 0 & x < 0 \end{cases}$

besitzt.

Die Exponentialverteilung hat einen reellen Parameter λ. Er besitzt den Charakter einer Ausfallrate und 1 / λ den einer Lebensdauer. Um ihre Normierbarkeit zu garantieren, wird λ > 0 gefordert.

Eine (vor allem im angelsächsischen Raum übliche) alternative Parametrisierung führt zur Wahrscheinlichkeitsdichte

$f_{\mu} (x)= \begin{cases}\displaystyle \frac{1}{\mu} \mathrm{e}^{-\frac{x}{\mu}} & x\geq 0 \\ 0 & x < 0 \end{cases}$.

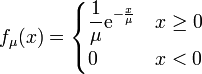Die Beziehung zur obigen Parametrisierung ist dabei einfach μ = 1 / λ. Um Missverständnissen vorzubeugen, wird empfohlen, den Erwartungswert explizit anzugeben, also von einer Exponentialverteilung mit Erwartungswert 1 / λ zu sprechen.

Eigenschaften

Den maximalen Wert nimmt die Dichtefunktion der Exponentialverteilung bei 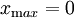$x_{\operatorname max} = 0$ ein, er beträgt dort $f_{\operatorname max} = \lambda$.

Verteilungsfunktion der Exponentialverteilung mit verschiedenen Werten für λ

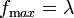Median

Die Exponentialverteilung besitzt ihren Median bei

$\tilde{x} = \frac{\ln 2}{\lambda}$.

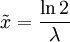Verteilungsfunktion

Die kumulierte Verteilungsfunktion der Exponentialverteilung ist

$F(x)=\begin{cases}\displaystyle \int\limits_{0}^x f_{\lambda}(t)\ {\rm d}t = 1-\mathrm{e}^{-\lambda x}& x\geq 0 \\ 0 & x < 0 \end{cases}$.

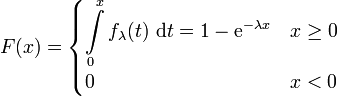Erwartungswert

Die Exponentialverteilung besitzt den Erwartungswert $\frac{1}{\lambda}$, denn

$\operatorname{E}(X) = \int\limits_0^\infty \lambda x \mathrm{e}^{-\lambda x} \operatorname{d}x = \frac{1}{\lambda}$.

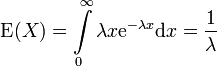Varianz

Die Varianz ergibt sich analog mittels

$\operatorname{Var}(X) = \int\limits_0^\infty \left( x-\frac{1}{\lambda}\right)^2\lambda \mathrm{e}^{-\lambda x}\operatorname{d}x = \lambda\int\limits_0^\infty x^2 \mathrm{e}^{-\lambda x}\operatorname{d}x - 2\int\limits_0^\infty x \mathrm{e}^{-\lambda x}\operatorname{d}x + \frac{1}{\lambda}\int\limits_0^\infty \mathrm{e}^{-\lambda x}\operatorname{d}x = \frac{1}{\lambda^2}$.

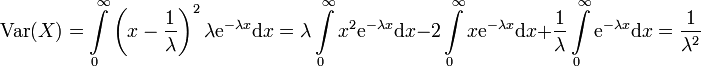Standardabweichung

Für die Standardabweichung ergibt sich

$\sigma = \sqrt{\operatorname{Var}(X)} = \sqrt{\frac{1}{\lambda^2}} = \frac{1}{\lambda}$.

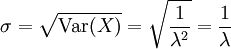Variationskoeffizient

Aus Erwartungswert und Varianz erhält man unmittelbar den Variationskoeffizienten

$\operatorname{VarK}(X) = \frac{\sqrt{\sigma^2(X)}}{\operatorname{E}(X)}=\frac{\sqrt{\operatorname{Var}(X)}}{\operatorname{E}(X)} \Leftrightarrow\operatorname{VarK}(X) = 1$

Schiefe

Die Schiefe besitzt unabhängig vom Parameter λ immer den Wert 2.

Charakteristische Funktion

Die charakteristische Funktion hat die Form

$\phi_{X}(t) = \frac{\lambda}{\lambda-\operatorname{i}t}$.

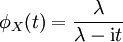Momenterzeugende Funktion

Die momenterzeugende Funktion der Exponentialverteilung ist

$m_{X}(t) = \frac{\lambda}{\lambda-t}$.

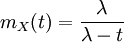Überlebenswahrscheinlichkeit

Da die Exponentialverteilung auch als Lebensdauerverteilung verwendet wird, ist es möglich, damit zusammenhängende Größen wie Überlebenswahrscheinlichkeit, die Restlebensdauer und die Ausfallrate mit Hilfe der Verteilungsfunktion anzugeben. So nennt man das Komplement der Verteilungsfunktion die Überlebenswahrscheinlichkeit

$P(X\operatorname>x) = 1-F(x) = \mathrm{e}^{-\lambda x}$.

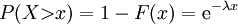Damit ergibt sich unmittelbar die auf einen Zeitpunkt x₀ bezogene bedingte Überlebenswahrscheinlichkeit

$P(X>x_{0}+x | X>x_{0}) = \frac{\mathrm{e}^{-\lambda (x_{0}+x)}}{\mathrm{e}^{-\lambda x_{0}}} = \mathrm{e}^{-\lambda x}$.

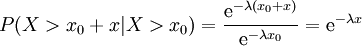Die Exponentialverteilung ist also eine gedächtnislose Lebensdauerverteilung, d.h. die Überlebenswahrscheinlichkeit in Bezug auf einen bestimmten Zeitpunkt ist unabhängig vom bisher erreichten Alter. Im Gegensatz zur Weibull-Verteilung kann die Exponentialverteilung also nur für sogenannte ermüdungsfreie Systeme verwendet werden

Die Ausfallrate r(x) ergibt sich zu

$r(x) = \frac{f(x)}{1-F(x)} = \frac{\lambda \mathrm{e}^{-\lambda x}}{\mathrm{e}^{-\lambda x}} = \lambda$.

Sie ist für die Exponentialverteilung zeitlich und räumlich konstant.

Gedächtnislosigkeit

Die Exponentialverteilung ist im folgenden Sinne „gedächtnislos“:

$P(X \ge x + t \, | \, X \ge x) = P(X \ge t)$

Das bedeutet: Ist bekannt, dass eine exponentialverteilte Zufallsvariable X den Wert x überschreitet, so ist die Wahrscheinlichkeit, dass sie x um mindestens t überschreitet genau so groß wie die, dass eine exponentialverteilte Zufallsvariable (mit gleichem Parameter λ) den Wert t überschreitet. Dieses Verhalten wird auch Markov-Eigenschaft genannt.

Die Gedächtnislosigkeit ist sogar eine definierende Eigenschaft der Exponentialverteilung; diese ist die einzig mögliche stetige Verteilung mit dieser Eigenschaft. Dies folgt direkt mit der Definition der bedingten Erwartung und der Cauchy-Funktionalgleichung. Das diskrete Pendant hierzu ist die geometrische Verteilung als einzig mögliche diskrete gedächtnislose Verteilung.

Weitere Eigenschaften

Sind 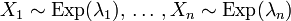$X_1\sim\mathrm{Exp}(\lambda_1) , \, \ldots \, , X_n\sim\mathrm{Exp}(\lambda_n)$ stochastisch unabhängig, so ist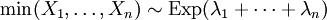 $\min(X_1,\ldots,X_n)\sim\operatorname{Exp}(\lambda_1+\dotsb+\lambda_n)$

Beziehung zu anderen Verteilungen

Beziehung zur stetigen Gleichverteilung

Wenn X eine auf dem Intervall [0, 1] gleichverteilte stetige Zufallsvariable ist, dann genügt 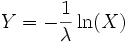$Y=-\frac{1}{\lambda}\ln(X)$ der Exponentialverteilung mit dem Parameter λ.

Beziehung zur geometrischen Verteilung

In Analogie zur diskreten geometrischen Verteilung bestimmt die stetige Exponentialverteilung die Wartezeit bis zum ersten Eintreffen eines seltenen Poisson-verteilten Ereignisses; die geometrische Verteilung kann also als diskretes Äquivalent zur Exponentialverteilung betrachtet werden.

Beziehung zur Gammaverteilung

• Die Verallgemeinerung der Exponentialverteilung, d. h. die Wartezeit bis zum Eintreffen des n-ten seltenen Poisson-verteilten Ereignisses wird mit der Gamma-Verteilung beschrieben. Die Exponentialverteilung mit Parameter λ ist also identisch mit der Gamma-Verteilung mit Parametern 1 und λ. Die Exponentialverteilung besitzt demnach auch alle Eigenschaften der Gammaverteilung. Insbesondere ist die Summe von n unabhängigen, $\operatorname{Exp}(\lambda)$-verteilten Zufallsvariablen Gamma- oder Erlangverteilt mit Parametern n und λ.
• Die Exponentialverteilung ergibt sich aus der Gamma-Verteilung für p = 1.

• Die Faltung von Exponential-Verteilungen mit demselben λ ergibt eine Gamma-Verteilung.

Beziehung zur Pareto-Verteilung

Wenn X Pareto-verteilt 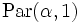$\operatorname{Par}(\alpha,1)$ mit Parametern α und 1 ist,dann ist logX exponentialverteilt 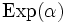$\operatorname{Exp}(\alpha)$ mit dem Parameter α.

Beziehung zur Poisson-Verteilung

Die Abstände zwischen dem Eintreten seltener Ereignisse können häufig mit der Exponentialverteilung beschrieben werden. Insbesondere gilt, dass der Abstand zwischen zwei aufeinanderfolgenden 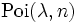$\operatorname{Poi}(\lambda,n)$ Poisson-verteilten Ereignissen 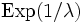$\operatorname{Exp}(1/\lambda)$ exponentialverteilt mit dem Parameter 1 / λ ist.

Herleitung: Sei w eine Orts- oder Zeitvariable und g die kleine konstante Eintretenshäufigkeit von Ereignissen im Einheitsintervall von w. Dann findet man mit den poissonschen Annahmen die Wahrscheinlichkeit für das nächste Eintreten eines Ereignisses im kleinen Intervall [w,w + Δw] als Produkt der Wahrscheinlichkeit, kein Ereignis bis w und eins im Intervall [w,w + Δw] zu haben:

$P_1(w+\Delta w) = \mathrm{e}^{-g \cdot w}\cdot g \Delta w$

Daraus ergibt sich nach Division durch Δw die Wahrscheinlichkeitsdichte 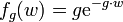$f_{g} (w)= g \mathrm{e}^{-g \cdot w}$ der Exponentialverteilung mit g als Ereignisrate und 1/g als mittlerem Ereignisabstand.

Beziehung zur Erlang-Verteilung

• Für einen Poisson-Prozess wird die zufällige Anzahl der Ereignisse bis zu einem definierten Zeitpunkt mittels Poisson-Verteilung bestimmt, die zufällige Zeit bis zum n-ten Ereignis ist Erlang-verteilt. Im Fall n = 1 geht diese Erlang Verteilung in eine Exponentialverteilung über 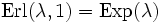$\operatorname{Erl}(\lambda,1)=\operatorname{Exp}(\lambda)$, mit der die Zeit bis zum ersten zufälligen Ereignis sowie die Zeit zwischen zwei aufeinanderfolgenden Ereignissen bestimmt werden kann.

• Die Summe von n unabhängigen $\operatorname{Exp}(\lambda)$ exponentialverteilten Zufallsgrößen genügt der Erlang-Verteilung n-ter der Ordnung $\operatorname{Erl}(\lambda,n)$.

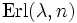Beziehung zur Weibull-Verteilung

• Mit β = 1 geht die Weibull-Verteilung in die Exponentialverteilung über. Mit anderen Worten: Die Exponentialverteilung behandelt Probleme mit konstanter Ausfallrate λ. Untersucht man jedoch Fragestellungen mit steigender α > 1 oder fallender α < 1 Ausfallrate, dann geht man von der Exponentialverteilung zur Weibull-Verteilung über.
• Wenn X exponential-verteilt ist, dann ist X^α Weibull-verteilt.

Beziehungen zur χ²-Verteilung

Die χ²-Verteilung geht für n = 2 in die Exponentialverteilung mit dem Parameter $\lambda=\frac{1}{2}$ über.

Anwendungsbeispiel

Die Exponentialverteilung ist eine typische Lebensdauerverteilung. So ist beispielsweise die Lebensdauer von elektronischen Bauelementen häufig annähernd exponentialverteilt. Hierbei spielt besonders die Gedächtnislosigkeit eine bedeutende Rolle: die Wahrscheinlichkeit, dass ein x Tage altes Bauelement noch mindestens t Tage hält, ist demnach genauso groß wie die, dass ein neues Bauelement überhaupt t Tage hält. Charakteristisch bei der Exponentialverteilung ist die konstante Ausfallrate λ.

Dies ist zum Beispiel bei Glühlampen nur annähernd richtig, da diese nur beim Einschalten stark beansprucht werden. Auf Lebewesen darf ebenfalls keine Exponentialverteilung angewendet werden, sonst wäre zum Beispiel die Wahrscheinlichkeit, dass ein Achtzigjähriger noch weitere Fünfzig Jahre lebt, genauso hoch wie die, dass ein Neugeborener das fünfzigste Lebensjahr erreicht.

Beispiel: In einer Elektronikfirma werden Funkwecker produziert. Im Rahmen der Qualitätssicherung wird anhand von Reklamationen die Funktionsdauer der Wecker untersucht. Es stellt sich heraus, dass durchschnittlich pro Tag 5 Promille der Wecker unabhängig von ihrem Alter ausfallen.

Die Zufallsgröße X = "Zeitdauer der Funktionsfähigkeit eines Funkweckers in Tagen" ist also exponentialverteilt mit der Ausfallrate λ = 0,005. Entsprechend beträgt die durchschnittliche Zeitdauer, bis ein Wecker ausfällt, 1 / λ = 200 Tage.

Die Wahrscheinlichkeit, dass ein Wecker höchstens (noch) 20 Tage hält, ist

$1-\mathrm{e}^{-0,005 \cdot 20} = 0,0952$

d.h. nach 20 Tagen sind durchschnittlich ca. 10 % der Wecker ausgefallen.

Entsprechend ist der Anteil der Wecker, die mindestens 180 Tage aushalten,

$1-(1-\mathrm{e}^{-0,005 \cdot 180}) = 1-0,5934 = 0,4066$

also halten durchschnittlich ca. 40% der Wecker länger als 180 Tage.

Obwohl bei einer exponentialverteilten Lebensdauerverteilung am Anfang absolut betrachtet mehr Geräte ausfallen, ist die Ausfallrate konstant: in jedem Zeitintervall fallen relativ betrachtet immer gleich viele Geräte aus. Dieser Umstand darf nicht mit den Frühausfällen der Badewannenkurve verwechselt werden. Hier ist zu Beginn die Ausfallrate λ höher und nicht konstant über die Lebensdauer. Zur Beschreibung der Badewannenkurve ist eine andere Lebensdauerverteilung (Weibull-Verteilung) notwendig.

Zufallszahlen

Zur Erzeugung exponentialverteilter Zufallszahlen bietet sich die Inversionsmethode an.

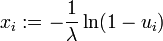Die nach dem Simulationslemma zu bildende Inverse der Verteilungsfunktion F(x) = 1 − e ^{− λx} lautet hierbei $F^{-1}(y) = - {1 \over \lambda} \ln ( 1 - y )$. Zu einer Folge von Standardzufallszahlen u_i lässt sich daher eine Folge $x_i := - { 1 \over \lambda } \ln ( 1 - u_i )$ exponentialverteilter Zufallszahlen berechnen. Einfacher kann stattdessen auch $x_i := - { 1 \over \lambda } \ln ( u_i )$ gerechnet werden.

Siehe auch

• Mortalität (Übergang von der Exponentialverteilung zur Weibull-Verteilung)

Weblinks

• Universität Konstanz – Interaktive Animation

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-Mandelbrot

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | Zeta

 

Kontinuierliche univariate Verteilungen

Kontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-Halbkreis

Kontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambda

Kontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | Voigt

 

Multivariate Verteilungen

Diskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet Multinomial

Kontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-Gamma

Multivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart