Gefilterte Rückprojektion

Vergleich der Bildqualität, SPECT-Aufnahme von Becken und Blase: iterative rekonstruktion links und gefilterter Rückprojektion rechts. Die bei sehr hoher und sehr niedriger Aktivität vorhandenen Artefakte sind deutlich erkennbar

Artefakte bei der Bildrekonstruktion mit der gefilterten Rückprojektion in der CT: Da die Röntgenstrahlung durch Goldplomben vollständig absorbiert wird, wird die Bildinformation hinter dem Zahn zerstört, was zur Artefaktbildung führt.

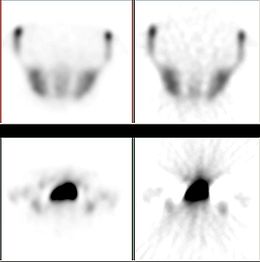
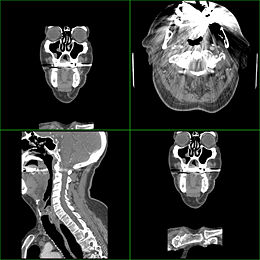
Die gefilterte Rückprojektion (auch FBP für filtered Backprojection) ist ein auf der Radon-Transformation beruhendes Verfahren zur Bildrekonstruktion, das in erster Linie in der Computertomographie verwendet wird. Das Verfahren hat den großen Vorteil, dass es schnell ist, da es wenig Rechenleistung benötigt. Jedoch können Fehler des Abbildungssystems nicht korrigiert werden. In der SPECT wie auch in der PET wurde sie mittlerweile von den iterativen Rekonstruktionsverfahren verdrängt.

Ein Beispiel soll den Algorithmus verdeutlichen.

Man stelle sich ein von vorne beleuchtetes Aquarium vor, bei dem sich die Konturen der Fische an einer dahinter befindlichen Leinwand abbilden. Führt man Lichtquelle und Leinwand in gleichen Winkelschritten um das Aquarium herum, erhält man viele Projektionen der Fische auf der Leinwand. Um aus diesen Daten hinterher die Position der Fische im Aquarium zu bestimmen, nimmt man jede einzelne der aufgenommenen Projektionen und projiziert sie auf das Volumen des Aquariums zurück (daher der Name des Verfahrens). Es ist klar, dass hierbei die Tiefeninformation nicht berücksichtigt wird, d.h. das endlich tiefe Bild des Fisches auf der Leinwand wird in Projektionsrichtung über das Bild verschmiert. Dieser Fehler lässt sich jedoch durch Anwendung eines geeigneten Bildfilters bei der Reprojektion wirkungsvoll unterdrücken.

Die point spread function der ungefilterten Rückprojektion ist 1 / r, wo r der Betrag im Ortsraum ist; das bedeutet, wenn das abzubildende Objekt nur aus einem Punkt mit den Koordinaten $\left(x',y',z'\right)$ besteht (Delta-Distribution), so erhält die ungefilterte Rückprojektion als Bild ein Signal am Ort $\left(x,y,z\right)$, das proportional zu $\frac{1}{\sqrt{(x-x')^2+(y-y')^2+(z-z')^2}}$ ist. Die "Filterung" entspricht mathematisch einer Faltung. Mit Hilfe des Faltungssatzes kann entfaltet werden, indem das rückprojizierte Bild in den Fourierraum transformiert, mit $|k|=\sqrt{k_x^2+k_y^2+k_z^2}$, dem Betrag im Fourierraum, multipliziert und anschließend wieder zurück in die Ortsraum transformiert wird. Gemäß dem Abtasttheorem kann der Filter bei einer bestimmten Raumfrequenz abgeschnitten werden. Außerdem ist zu beachten, dass Daten einer Computertomographie diskret vorliegen und nicht, wie mathematisch eigentlich nötig, kontinuierlich. Deshalb ist das CT nicht "exakt" und es gibt nicht den Filter, da beispielsweise zwischen den einzelnen diskreten Punkten gemittelt (Shepp-Logan Filter) oder nicht (Ram-Lak Filter) werden kann. Je nachdem, welchen Filter man benutzt, wird das Bild entweder kontrastreicher, aber verrauschter oder kontrastärmer, aber rauschreduzierter.

Siehe auch

Dekonvolution

Quellen

• Universität Giessen, Klinik für Nuklearmedizin
• Universität Freiburg (PDF-Datei; 1,44 MB)
• Uni Bonn
• W. Schlegel, J.Bille (Hrsg.): Medizinische Physik 2. Springer, Berlin Heidelberg New York 2002, ISBN 3-540-65254-X