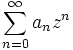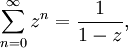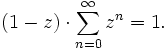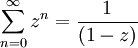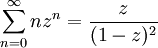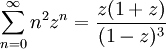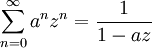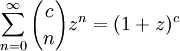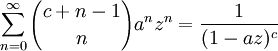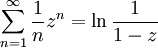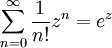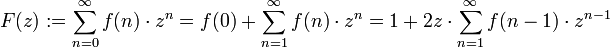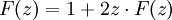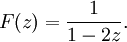Generierendenfunktion

In verschiedenen Teilgebieten der Mathematik versteht man unter der erzeugenden Funktion einer Folge a_n die formale Potenzreihe

$\sum_{n=0}^{\infty} a_n z^n$

Ein einfaches Beispiel ist die erzeugende Funktion der konstanten Folge $1, 1, 1, \ldots$

$\sum_{n=0}^{\infty} z^n = \frac{1}{1-z},$

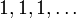
die Gleichheit gilt nur für | z | < 1 und folgt aus der Beobachtung

$(1-z) \cdot \sum_{n=0}^{\infty} z^n = 1.$

Wegen der Verwendung formaler Potenzreihen spielen Konvergenzfragen keine Rolle - z ist lediglich ein Symbol. Diese explizitere Darstellung der Potenzreihe ermöglicht oft Rückschlüsse auf die Folge.

Explizite Formeln für einige wichtige Potenzreihen

Es gelten folgende Identitäten:

• $\sum_{n=0}^{\infty} z^n = \frac{1}{(1-z)}$
• $\sum_{n=0}^{\infty} n z^n = \frac{z}{(1-z)^2}$
• $\sum_{n=0}^{\infty} n^2 z^n = \frac{z(1+z)}{(1-z)^3}$
• $\sum_{n=0}^{\infty} a^n z^n = \frac{1}{1 - az}$
• $\sum_{n=0}^{\infty} {c \choose n} z^n = (1 + z)^c$
• $\sum_{n=0}^{\infty} {c + n - 1 \choose n} a^n z^n = \frac{1}{(1-az)^c}$
• $\sum_{n=1}^{\infty} \frac{1}{n}z^n = \ln \frac{1}{1-z}$
• $\sum_{n=0}^{\infty} \frac{1}{n!}z^n = e^z$

Anwendung

Erzeugende Funktionen liefern ein wichtiges Hilfsmittel für das Lösen von Rekursionen und Differenzengleichungen sowie der Berechnung von Partitionen. Eine Indexverminderung innerhalb der Folge entspricht einer Multiplikation der erzeugenden Funktion mit z. Angenommen, wir haben die Rekursion 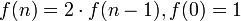$f(n) = 2\cdot f(n-1), f(0) = 1$ zu lösen, dann ist 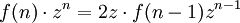$f(n)\cdot z^n = 2z\cdot f(n-1) z^{n-1}$, und es gilt für die erzeugende Funktion

$F(z) := \sum_{n=0}^\infty f(n) \cdot z^{n} = f(0) + \sum_{n=1}^\infty f(n) \cdot z^{n}= 1 + 2z\cdot \sum_{n=1}^\infty f(n-1) \cdot z^{n-1}$

also

$F(z) = 1+ 2z \cdot F(z)$

Auflösen nach F liefert

$F(z) = \frac{1}{1 - 2z}.$

Wir wissen aber aus dem vorhergehenden Abschnitt, dass dies der Reihe 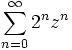$\sum_{n=0}^\infty 2^n z^n$ entspricht, also gilt f(n) = 2ⁿ nach Koeffizientenvergleich.

Verschiedene Typen von erzeugenden Funktionen

Es gibt neben der gewöhnlichen erzeugenden Funktion noch weitere Typen von erzeugenden Funktionen. Manchmal erweist es sich als zweckmäßig, Folgen mit Hilfe der folgenden zwei Arten von erzeugenden Funktionen zu betrachten.

Exponentiell erzeugende Funktion

Die exponentiell erzeugende Funktion (oder erzeugende Funktion vom Exponentialtyp) einer Folge a_n ist die Reihe $\sum_{n=0}^\infty \frac{a_n}{n!} z^n$.

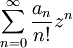Zum Beispiel ist die Exponentialfunktion e^z die exponentiell erzeugende Funktion der Folge $1, 1, 1, \ldots$

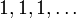
Dirichlet-erzeugende Funktion

Die Dirichlet-erzeugende Funktion einer Folge a_n ist die Reihe 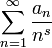$\sum_{n=1}^{\infty} \frac{a_n}{n^s}$. Sie ist benannt nach Peter Gustav Lejeune Dirichlet.

Zum Beispiel ist die Riemannsche Zetafunktion 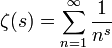$\zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s}$ die Dirichlet-erzeugende Funktion der Folge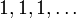 $1, 1, 1, \ldots$

Siehe auch

• Rekursion
• Differenzengleichung
• Momenterzeugende Funktion
• Wahrscheinlichkeitserzeugende Funktion

Literatur

• Martin Aigner: Diskrete Mathematik. 5. Auflage. vieweg, Wiesbaden 2004. ISBN 3-528-47-268-5
• Herbert S. Wilf: generatingfunctionology, 3. Auflage, A. K. Peters Ltd. 2005, ISBN 978-1-56881-279-3; 2. Auflage im PDF
• Wikibook: Lineare Rekurrenzen, Potenzreihen und ihre erzeugenden Funktionen