- Gesamtenergiedichte
-
Das plancksche Strahlungsgesetz
Der Artikel plancksches Strahlungsgesetz erläutert die physikalische Bedeutung des Strahlungsgesetzes. Für die hier behandelte mathematische Darstellung des Gesetzes existieren zahlreiche verschiedene Varianten, je nachdem ob das Gesetz in Abhängigkeit von der Frequenz oder der Wellenlänge formuliert werden soll, ob die Intensität der Strahlung in eine bestimmte Richtung oder die Abstrahlung in den gesamten Halbraum betrachtet werden soll, ob Strahlgrößen, Energiedichten oder Photonenzahlen beschrieben werden sollen. Diese verschiedenen Formen werden im Folgenden in ihrem gegenseitigen Zusammenhang dargestellt und erläutert. Die Formelsammlung enthält auch unmittelbar aus dem planckschen Strahlungsgesetz abgeleitete Gesetze wie z.B. das Stefan-Boltzmann-Gesetz.
Wie bei radiometrischen Größen üblich, können auch zur Beschreibung des Spektrums eines Schwarzen Körpers verschiedene Strahlungsgrößen verwendet werden. Die hier benutzten Bezeichnungen und Symbole folgen der DIN EN ISO 9288 (August 1996). Der obere Index
 weist jeweils darauf hin, dass die betreffende Größe hier speziell die Eigenschaften eines Schwarzen Körpers beschreibt. Die folgenden Formeln gelten für die Strahlung im Vakuum. Bei Strahlung in ein Medium mit der Brechzahl n sind die Vakuumlichtgeschwindigkeit c durch c / n und die Wellenlänge λ durch λ / n zu ersetzen, während die Frequenz ν unverändert bleibt.[1]
weist jeweils darauf hin, dass die betreffende Größe hier speziell die Eigenschaften eines Schwarzen Körpers beschreibt. Die folgenden Formeln gelten für die Strahlung im Vakuum. Bei Strahlung in ein Medium mit der Brechzahl n sind die Vakuumlichtgeschwindigkeit c durch c / n und die Wellenlänge λ durch λ / n zu ersetzen, während die Frequenz ν unverändert bleibt.[1]Man unterscheidet
- spektrale Größen, welche die Frequenz- bzw. Wellenlängenabhängigkeiten explizit beschreiben
- Gesamtgrößen, welche über alle Frequenzen bzw. Wellenlängen integriert sind
sowie
- gerichtete Größen, welche die Richtungsabhängigkeiten explizit beschreiben
- hemisphärische Größen, welche über alle Richtungen des Halbraums integriert sind.
Spektrale Strahldichte
Die spektrale Strahldichte
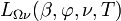 liefert die detaillierteste Darstellung der Strahlungseigenschaften eines Strahlers. Sie beschreibt explizit die Richtungsabhängigkeit und die Frequenz- (oder Wellenlängen‑)abhängigkeit der abgegebenen Strahlung. Aus der spektralen Strahldichte lassen sich die anderen Strahlungsgrößen durch Integration über die Richtungen und/oder Frequenzen ableiten.
liefert die detaillierteste Darstellung der Strahlungseigenschaften eines Strahlers. Sie beschreibt explizit die Richtungsabhängigkeit und die Frequenz- (oder Wellenlängen‑)abhängigkeit der abgegebenen Strahlung. Aus der spektralen Strahldichte lassen sich die anderen Strahlungsgrößen durch Integration über die Richtungen und/oder Frequenzen ableiten.Für die spektrale Strahldichte
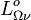 eines Schwarzen Körpers der absoluten Temperatur T gilt
eines Schwarzen Körpers der absoluten Temperatur T giltin der Frequenzdarstellung:
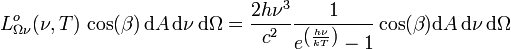
SI-Einheit von 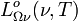 : W m-2 Hz-1 sr-1,
: W m-2 Hz-1 sr-1,in der Wellenlängendarstellung:
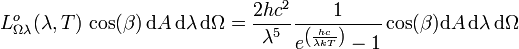
SI-Einheit von 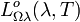 : W m-2 μm-1 sr-1.
: W m-2 μm-1 sr-1.
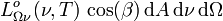 ist die Strahlungsleistung, die vom Flächenelement dA im Frequenzbereich zwischen ν und ν + dν in das zwischen den Azimutwinkeln φ und φ+dφ sowie den Polarwinkeln β und β+dβ aufgespannte Raumwinkelelement dΩ abgestrahlt wird. Weiter sind h das plancksche Wirkungsquantum, c die Lichtgeschwindigkeit und k die Boltzmannkonstante.
ist die Strahlungsleistung, die vom Flächenelement dA im Frequenzbereich zwischen ν und ν + dν in das zwischen den Azimutwinkeln φ und φ+dφ sowie den Polarwinkeln β und β+dβ aufgespannte Raumwinkelelement dΩ abgestrahlt wird. Weiter sind h das plancksche Wirkungsquantum, c die Lichtgeschwindigkeit und k die Boltzmannkonstante.Der Kosinusfaktor berücksichtigt den Umstand, dass bei Abstrahlung in eine beliebige durch φ und β gegebene Richtung nur die auf dieser Richtung senkrecht stehende Projektion cos(β)dA der Fläche dA als effektive Strahlfläche auftritt. Die spektrale Strahldichte
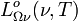 selbst muss im Falle des Schwarzen Körpers aus thermodynamischen Gründen richtungsunabhängig sein (Begründung: Ist der Schwarze Körper einer Hohlraumstrahlung derselben Temperatur ausgesetzt, so absorbiert er die auf ihn treffende Strahlung vollständig, muss die absorbierte Strahlung aber gleichzeitig durch selbst emittierte Strahlung ersetzen, um das thermische Gleichgewicht zu erhalten. Die spektrale Strahldichte der Hohlraumstrahlung muss im Gleichgewicht richtungsunabhängig sein, und da die vom Schwarzen Körper emittierte Strahlung dieselbe Strahldichte haben muss, ist sie ebenfalls richtungsunabhängig). Der Schwarze Körper strahlt also völlig diffus, er ist ein Lambert-Strahler.
selbst muss im Falle des Schwarzen Körpers aus thermodynamischen Gründen richtungsunabhängig sein (Begründung: Ist der Schwarze Körper einer Hohlraumstrahlung derselben Temperatur ausgesetzt, so absorbiert er die auf ihn treffende Strahlung vollständig, muss die absorbierte Strahlung aber gleichzeitig durch selbst emittierte Strahlung ersetzen, um das thermische Gleichgewicht zu erhalten. Die spektrale Strahldichte der Hohlraumstrahlung muss im Gleichgewicht richtungsunabhängig sein, und da die vom Schwarzen Körper emittierte Strahlung dieselbe Strahldichte haben muss, ist sie ebenfalls richtungsunabhängig). Der Schwarze Körper strahlt also völlig diffus, er ist ein Lambert-Strahler.Bei der Umrechnung zwischen Frequenz- und Wellenlängendarstellung ist zu beachten, dass wegen
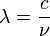 gilt:
gilt: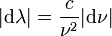 und
und 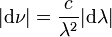
Die spektrale Strahldichte ist eine spektrale gerichtete Größe.
Spektrale spezifische Ausstrahlung
Integriert man die spektrale Strahldichte über alle Richtungen des Halbraums, in welchen das betrachtete Flächenelement abstrahlt, so erhält man die spektrale spezifische Ausstrahlung in den Halbraum
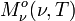 , für die gilt:
, für die gilt: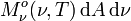
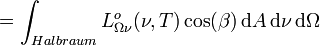
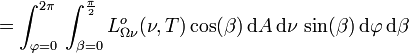
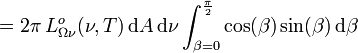
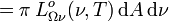 ,
,so dass also in der Frequenzdarstellung:
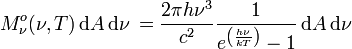
SI-Einheit von 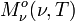 : W m-2 Hz-1
: W m-2 Hz-1und in der Wellenlängendarstellung:
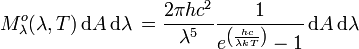
SI-Einheit von 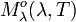 : W m-2 μm-1.
: W m-2 μm-1.
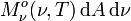 ist die Strahlungsleistung, die vom Flächenelement dA im Frequenzbereich zwischen ν und ν + dν in den Halbraum abgestrahlt wird.
ist die Strahlungsleistung, die vom Flächenelement dA im Frequenzbereich zwischen ν und ν + dν in den Halbraum abgestrahlt wird.Die spektrale spezifische Ausstrahlung ist eine spektrale hemisphärische Größe.
Gesamtstrahldichte
Integriert man die spektrale Strahldichte nicht über die Richtungen, sondern über alle Frequenzen, so erhält man die Gesamtstrahldichte
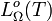 , für die gilt:
, für die gilt: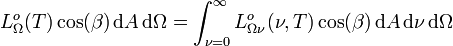
Die Auswertung des Integrals liefert wegen
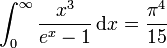 :
: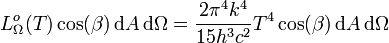
SI-Einheit von 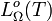 : W m-2 sr-1.
: W m-2 sr-1.
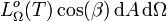 ist die Strahlungsleistung, die vom Flächenelement dA auf allen Frequenzen in das in der Richtung β gelegene Raumwinkelelement dΩ abgestrahlt wird.
ist die Strahlungsleistung, die vom Flächenelement dA auf allen Frequenzen in das in der Richtung β gelegene Raumwinkelelement dΩ abgestrahlt wird.Die Gesamtstrahldichte ist eine gerichtete Gesamtgröße.
Spezifische Ausstrahlung, Stefan-Boltzmann-Gesetz
Hauptartikel: Stefan-Boltzmann-Gesetz
Integriert man die spektrale spezifische Ausstrahlung über alle Frequenzen oder die Gesamtstrahldichte über alle Richtungen des Halbraums, so erhält man die spezifische Ausstrahlung
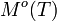 , für die gilt
, für die gilt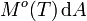
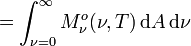
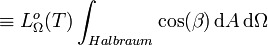
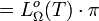
so dass
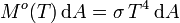
SI-Einheit von 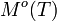 : W m-2,
: W m-2,mit der Stefan-Boltzmann-Konstanten
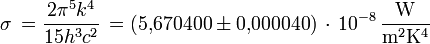 (gemäß CODATA 2006). Bei Strahlung in ein Medium mit der Brechzahl n ist die Vakuumlichtgeschwindigkeit c durch c / n zu ersetzen, die spezifische Ausstrahlung erhöht sich daher um den Faktor n2.
(gemäß CODATA 2006). Bei Strahlung in ein Medium mit der Brechzahl n ist die Vakuumlichtgeschwindigkeit c durch c / n zu ersetzen, die spezifische Ausstrahlung erhöht sich daher um den Faktor n2.
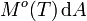 ist die Strahlungsleistung, die vom Flächenelement dA auf allen Frequenzen in den Halbraum abgestrahlt wird.
ist die Strahlungsleistung, die vom Flächenelement dA auf allen Frequenzen in den Halbraum abgestrahlt wird.Die spezifische Ausstrahlung ist eine hemisphärische Gesamtgröße.
Strahlungsfluss oder Strahlungsleistung
Integriert man die spezifische Ausstrahlung über die gesamte strahlende Fläche A, so erhält man die Strahlungsleistung
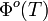 dieser Fläche, für die gilt:
dieser Fläche, für die gilt: ,
,so dass
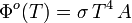
SI-Einheit von 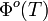 : W.
: W.
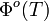 ist die Strahlungsleistung, die von der Fläche A auf allen Frequenzen in den Halbraum abgestrahlt wird.
ist die Strahlungsleistung, die von der Fläche A auf allen Frequenzen in den Halbraum abgestrahlt wird.Spektrale Energiedichte der Hohlraumstrahlung
Hauptartikel: Energiedichte, Hohlraumstrahlung
Ein geschlossener Hohlraum mit Wänden aus beliebigem Material, welche auf der Temperatur T gehalten werden, ist nach Erreichen des thermischen Gleichgewichts mit einer homogenen isotropen thermischen Strahlung erfüllt, deren Eigenschaften nur von der Temperatur T abhängen und die daher universalen Charakter hat.
Bringt man einen kleinen Schwarzen Körper in den Hohlraum, so muss die Hohlraumstrahlung nach Wiederherstellung des thermischen Gleichgewichts die gleiche sein wie vorher, da sie nur von T abhängt. Da der Schwarze Körper sämtliche auf ihn treffende Hohlraumstrahlung absorbiert, zur Erhaltung des Gleichgewichts aber gleichzeitig die gleiche Strahlung als Ersatz wieder emittieren muss, müssen die spektralen Strahldichten der Hohlraumstrahlung und der Strahlung des Schwarzen Körpers identisch sein. Die oben hergeleiteten Ausdrücke für die einzelnen Strahlgrößen gelten daher auch für die Hohlraumstrahlung. Darüber hinaus weist die Hohlraumstrahlung eine konstante räumliche Energiedichte auf.
Man betrachte einen halbkugelförmigen mit Hohlraumstrahlung der Temperatur T gefüllten Hohlraum. Da die Strahlgrößen dieselben sind wie bei der Emission durch einen Schwarzen Körper, ist die aus dem gesamten Halbraum stammende auf ein Flächenelement dA im Mittelpunkt der kreisförmigen Grundfläche treffende Strahlungsleistung im Frequenzintervall zwischen ν und ν+dν gegeben durch die Formel zur spektralen spezifischen Ausstrahlung:
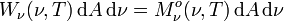 (*)
(*)Seien nun
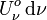 die Energiedichte im Frequenzintervall zwischen ν und ν+dν und
die Energiedichte im Frequenzintervall zwischen ν und ν+dν und 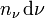 die Dichte der Photonen aus demselben Frequenzintervall:
die Dichte der Photonen aus demselben Frequenzintervall: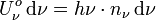
Da die Strahlung isotrop ist, kommen alle Richtungen gleich häufig vor. Der Anteil an Photonen, welcher aus dem Raumwinkelelement dΩ, d. h. aus Richtungen zwischen φ und φ + dφ sowie zwischen β und β + dβ, stammt, ist gegeben durch das Verhältnis von dΩ zum vollen Raumwinkel 4π. Die Dichte an Photonen mit Frequenzen zwischen ν und ν+dν, welche aus dem Raumwinkel dΩ stammen, ist daher
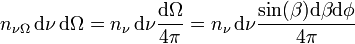
Von allen Photonen aus dem Frequenzintervall dν, welche aus der Richtung von dΩ kommen, treten jene durch die Fläche dA, welche sich in einem Zylinder befinden, der um den Winkel β in die Richtung von dΩ geneigt ist und dA zur Grundfläche hat. Pro Zeiteinheit dt treten jene Photonen durch dA, die sich in einem Zylinderstück der Länge cdt befinden. Sie treten also mit der Rate
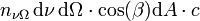
durch dA. Da jedes Photon die Energie hν trägt, tritt die Energie mit der Rate
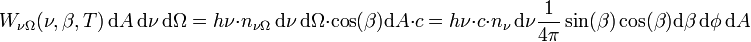
durch dA. Es treten Photonen aus dem gesamten oberen Halbraum durch dA; Integration über den Halbraum liefert
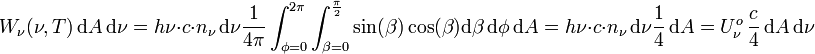
Vergleich mit (*) zeigt:
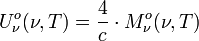
Es gilt also
in der Frequenzdarstellung:
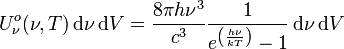
SI-Einheit von 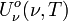 : J m-3 s oder anschaulicher J m-3 Hz-1,
: J m-3 s oder anschaulicher J m-3 Hz-1,in der Wellenlängendarstellung:
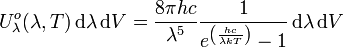
SI-Einheit von 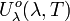 : J m-4 oder anschaulicher J m-3 μm-1.
: J m-4 oder anschaulicher J m-3 μm-1.
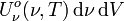 ist die Energie der thermischen Strahlung im Frequenzbereich zwischen ν und ν + dν, welche sich im Volumenelement dV eines Hohlraumstrahlers befindet.
ist die Energie der thermischen Strahlung im Frequenzbereich zwischen ν und ν + dν, welche sich im Volumenelement dV eines Hohlraumstrahlers befindet.Die spezifischen Funktionen haben jeweils ein Maximum, das temperaturabhängig ist - siehe Wiensches Verschiebungsgesetz. Wird die gesamte Strahlungsintensität für ein flächengleiches Rechteck betrachtet mit der Maximalintensität, so ist das Verhältnis Breite zu Maximalfrequenz (bzw. ...) temperaturunabhängig.
Gesamtenergiedichte der Hohlraumstrahlung
Integriert man die spektrale Energiedichte der Hohlraumstrahlung über alle Frequenzen, so erhält man die Gesamtenergiedichte Uo, für die gilt:
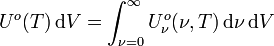
Auswertung des Integrals liefert:
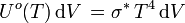
mit 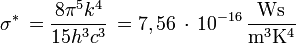 , SI-Einheit von Uo(T): J m-3.
, SI-Einheit von Uo(T): J m-3.
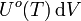 ist die Energie der thermischen Strahlung aller Frequenzen, welche sich im Volumenelement dV eines Hohlraumstrahlers befindet.
ist die Energie der thermischen Strahlung aller Frequenzen, welche sich im Volumenelement dV eines Hohlraumstrahlers befindet.Tabellarische Übersicht
spektrale Strahldichte: 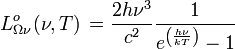
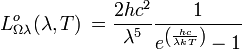
Einheit: W m-2 Hz-1 sr-1 Einheit: W m-2 μm-1 sr-1 spektrale spezifische Ausstrahlung: 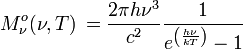
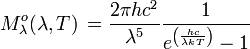
Einheit: W m-2 Hz-1 Einheit: W m-2 μm-1 Lage des Intensitätsmaximums (siehe Wiensches Verschiebungsgesetz): 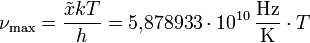 mit
mit 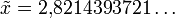
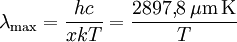 mit
mit 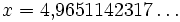
Einheit: Hz Einheit: μm Zusammenhang Maxima: 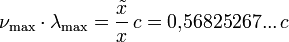
Einheit: m s-1 Gesamtstrahldichte: 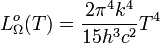
Einheit: W m-2 sr-1 spezifische Ausstrahlung ("Stefan-Boltzmann-Gesetz"): 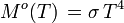 mit Stefan-Boltzmann-Konstante
mit Stefan-Boltzmann-Konstante 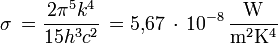
Einheit: W m-2 relative Breite eines äquivalenten intensitätskonstanten Rechtecks: 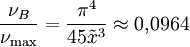
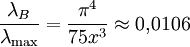
Einheit: - Einheit: - spektrale Energiedichte im Hohlraum: 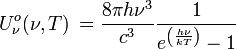
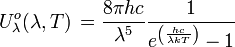
Einheit: J m-3 Hz-1 Einheit: J m-3 μm-1 Gesamtenergiedichte im Hohlraum: 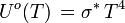 mit
mit 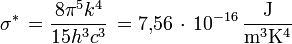
Einheit: J m-3
Statt der pro Zeiteinheit abgestrahlten Energie kann auch die pro Zeiteinheit abgestrahlte Anzahl von Photonen betrachtet werden. Da ein Photon der Frequenz ν bzw. der Wellenlänge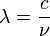 die Energie hν bzw.
die Energie hν bzw. 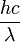 trägt, gilt:[2]
trägt, gilt:[2]spektrale Strahldichte: 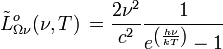
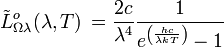
Einheit: Photonen s-1 m-2 Hz-1 sr-1 Einheit: Photonen s-1 m-2 μm-1 sr-1 spektrale spezifische Ausstrahlung: 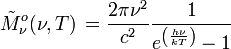
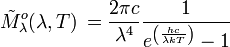
Einheit: Photonen s-1 m-2 Hz-1 Einheit: Photonen s-1 m-2 μm-1 Gesamtstrahldichte: 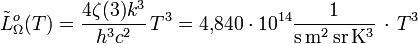
mit ζ(3) = 1,202056903... (riemannsche Zeta-Funktion) Einheit: Photonen s-1 m-2 sr-1 spezifische Ausstrahlung (Stefan-Boltzmann-Gesetz für die Photonenrate): 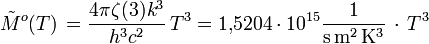
Einheit: Photonen s-1 m-2 spektrale Photonendichte im Hohlraum: 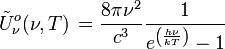
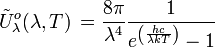
Einheit: Photonen m-3 Hz-1 Einheit: Photonen m-3 μm-1 Gesamtphotonendichte im Hohlraum: 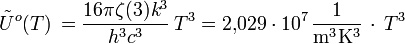
Einheit: Photonen m-3 Quellen
- Baehr/Stephan: Baehr H.D., Stephan K.: Wärme- und Stoffübertragung. 5. Auflage, Springer, Berlin 2006, ISBN 978-3-540-32334-1
- Tatum: Tatum J.B.: Stellar Atmospheres, chapter 2: Blackbody Radiation. On-line lecture notes (pdf 217 KB)
Wikimedia Foundation.
