Giugas Vermutung

Die Giuga-Zahlen sind nach dem Mathematiker Giuseppe Giuga benannte natürliche Zahlen mit speziellen Eigenschaften. Sie sind im Zusammenhang mit einer von ihm vermuteten Charakterisierung der Primzahlen von Bedeutung. Verwandt zu den Giuga-Zahlen sind die primär pseudovollkommenen Zahlen und die Carmichael-Zahlen.

Giugas Vermutung

Im Jahr 1950 äußerte G. Giuga die Vermutung, dass eine natürliche Zahl n genau dann eine Primzahl sei, wenn $\sum_{k=1}^{n-1} k^{n-1} \equiv -1 \pmod{n}$ gilt. Für Primzahlen folgt diese Eigenschaft aus dem kleinen Satz von Fermat. Bis heute ist ungeklärt, ob auch die umgekehrte Schlussrichtung gilt. Es ist also nicht bekannt, ob es auch zusammengesetzte Zahlen mit dieser Eigenschaft gibt. Nach einem Ergebnis aus dem Jahr 1994 müsste eine solche Zahl mehr als 10.000 Dezimalstellen haben.

Giugas Vermutung ist äquivalent zu folgender Aussage: Keine natürliche Zahl ist zugleich Giuga- und Carmichael-Zahl.

Definition

Eine zusammengesetzte Zahl n heißt Giuga-Zahl, wenn für alle Primteiler p von n gilt: p teilt $\frac{n}{p}-1$.

Die zu den Giuga-Zahlen verwandten Carmichael-Zahlen besitzen eine ähnliche Charakterisierung: Eine zusammengesetzte Zahl heißt Carmichael-Zahl, wenn für alle Primteiler p von n gilt: $\!\,p-1$ teilt $\frac{n}{p}-1$.

Äquivalente Charakterisierungen

Die Giuga-Zahlen lassen sich noch auf weitere Arten charakterisieren: Sei n eine zusammengesetzte Zahl und P die Menge der Primteiler von n. Dann gilt:

• Die Zahl n ist genau dann eine Giuga-Zahl, wenn gilt: $\sum_{k=1}^{n-1} k^{\varphi(n)}\equiv -1 \pmod {n}$.
• Die Zahl n ist genau dann eine Giuga-Zahl, wenn gilt: n ist quadratfrei und $\sum_{p\in P}\frac{1}{p} - \prod_{p\in P}\frac{1}{p} \in\mathbb{N}$

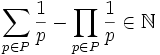
Dies zeigt die enge Beziehung der Giuga-Zahlen zu den primär pseudovollkommenen Zahlen, die durch 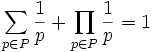$\sum_{p\in P}\frac{1}{p} + \prod_{p\in P}\frac{1}{p} = 1$ charakterisiert sind.

• Die Zahl n ist genau dann eine Giuga-Zahl, wenn gilt: $n B_{\varphi(n)} \equiv -1 \pmod{n}$.

Dabei bezeichnet $\varphi$ die Eulersche φ-Funktion und B die Bernoulli-Zahlen.

Bekannte Giuga-Zahlen

• 3 Faktoren:
  • 30 = 2 * 3 * 5
• 4 Faktoren:
  • 858 = 2 * 3 * 11 * 13
  • 1722 = 2 * 3 * 7 * 41
• 5 Faktoren:
  • 66.198 = 2 * 3 * 11 * 17 * 59
• 6 Faktoren:
  • 2.214.408.306 = 2 * 3 * 11 * 23 * 31 * 47.057
  • 24.423.128.562 = 2 * 3 * 7 * 43 * 3041 * 4447
• 7 Faktoren:
  • 432.749.205.173.838 = 2 * 3 * 7 * 59 * 163 * 1381 * 775.807
  • 14.737.133.470.010.574 = 2 * 3 * 7 * 71 * 103 * 67.213 * 713.863
  • 550.843.391.309.130.318 = 2 * 3 * 7 * 71 * 103 * 61.559 * 29.133.437
• 8 Faktoren:
  • 244.197.000.982.499.715.087.866.346 = 2 * 3 * 11 * 23 * 31 * 47.137 * 28.282.147 * 3.892.535.183
  • 554.079.914.617.070.801.288.578.559.178 = 2 * 3 * 11 * 23 * 31 * 47.059 * 2.259.696.349 * 110.725.121.051
  • 1.910.667.181.420.507.984.555.759.916.338.506 = 2 * 3 * 7 * 43 * 1831 * 138.683 * 2.861.051 * 1.456.230.512.169.437
• 10 Faktoren:
  • 4.200.017.949.707.747.062.038.711.509.670.656.632.404.195.753.751.630.609.228.764.416.142.557.211.582.098.432.545.190.323.474.818 = 2 * 3 * 11 * 23 * 31 * 47.059 * 2.217.342.227 * 1.729.101.023.519 * 8.491.659.218.261.819.498.490.029.296.021 * 58.254.480.569.119.734.123.541.298.976.556.403

Eigenschaften

• Alle Giuga-Zahlen sind quadratfrei.
• Alle Giuga-Zahlen sind abundant.
• Es existieren nur endlich viele Giuga-Zahlen mit einer vorgegebenen Anzahl von Primfaktoren.
• Es ist nicht bekannt, ob es unendlich viele Giuga-Zahlen gibt.
• Alle bekannten Giuga-Zahlen sind gerade. Eine ungerade Giuga-Zahl müsste aus mindestens 14 Primfaktoren bestehen. Da alle Carmichael-Zahlen ungerade sind, wäre auch Giugas Vermutung bewiesen, wenn man beweisen könnte, dass alle Giuga-Zahlen gerade sind.

Literatur

• G. Giuga: Su una presumibile proprietà caratteristica dei numeri primi. Ist. Lombardo Sci. Lett. Rend. A, 83:511-528, 1950
• T. Agoh: On Giuga’s conjecture. Manuscripta Math. 87(4): 501-510, 1995
• D. Borwein, J. M. Borwein, P. B. Borwein und R. Girgensohn: Giuga's Conjecture on Primality. Amer. Math. Monthly 103:40-50, 1996