- Gleichung dritten Grades
-
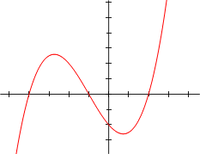 Graph einer Funktion 3. Grades; die Nullstellen (y=0) sind dort wo der Graph die x-Achse schneidet. Der Graph hat 2 Extremwerte.
Graph einer Funktion 3. Grades; die Nullstellen (y=0) sind dort wo der Graph die x-Achse schneidet. Der Graph hat 2 Extremwerte.Kubische Gleichungen sind algebraische Gleichungen dritten Grades, also Gleichungen der allgemeinen Form
mit
 und
und 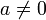 in der Unbekannten
in der Unbekannten 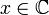 (siehe auch Polynom). Im Fall a = 0 handelt es sich höchstens noch um eine quadratische Gleichung.
(siehe auch Polynom). Im Fall a = 0 handelt es sich höchstens noch um eine quadratische Gleichung.Die kubische Gleichung lässt sich mit Kenntnis aller drei komplexen Nullstellen x1,x2,x3 auch so faktorisieren:
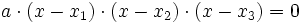 .
.
Geometrisch beschreibt die reelle Variante der kubischen Gleichung eine kubische Parabel in der x-y-Ebene. Die Schnittpunkte mit der x-Achse sind die reellen Nullstellen. Da die Parabel immer von
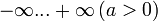 bzw. von
bzw. von 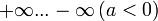 läuft und die Funktion stetig ist, muss es (nach dem Zwischenwertsatz) stets mindestens einen Schnittpunkt mit der x-Achse geben, d.h. mindestens eine reelle Nullstelle. Dies spiegelt sich auch in der algebraischen Behandlung wider.
läuft und die Funktion stetig ist, muss es (nach dem Zwischenwertsatz) stets mindestens einen Schnittpunkt mit der x-Achse geben, d.h. mindestens eine reelle Nullstelle. Dies spiegelt sich auch in der algebraischen Behandlung wider.Inhaltsverzeichnis
Lösungsansätze
Raten einer Lösung
Sind alle Vorfaktoren ganzzahlig, dann kann man versuchen, durch Polynomdivision zu einer einfacheren quadratischen Gleichung zu kommen, die mit klassischen Verfahren lösbar sind. Dazu braucht man eine bekannte Nullstelle.
Ist der führende Koeffizient a gleich 1, so kann man die ganzzahligen Teiler des letztens Faktors d durchprobieren (auch negative Werte!). Ist a von eins verschieden, so müssen alle Brüche, deren Zähler ein Teiler von d und deren Nenner ein Teiler von a ist, durchprobiert werden. Bei rationalen Vorfaktoren lässt sich eine Ganzzahligkeit durch Multiplikation der Gleichung mit dem kgV aller Nenner erreichen.
Reduktion der Gleichung auf eine Normalform
Es gibt eine Reihe äquivalenter Umformungen dieser Gleichung durch Verschieben und Skalieren des Arguments und Skalieren der Gleichung, die es erlauben, bestimmten Koeffizienten feste Werte zuzuweisen und damit das nachfolgende Lösungsverfahren zu vereinfachen. Üblicherweise wird der führende Koeffizient zu 1 und der quadratische zu 0 transformiert.
Dazu wird das Argument um ein vorerst beliebiges
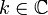 verschoben, x = z − k, und die Gleichung durch
verschoben, x = z − k, und die Gleichung durch 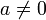 dividiert.
dividiert.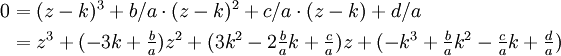 .
.
Mit
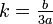 fällt das quadratische Glied weg und es bleibt
fällt das quadratische Glied weg und es bleibt .
.
Der einfachste und historisch älteste Lösungsweg beruht nun auf dem Ansatz
![z=\sqrt[3]{A}+\sqrt[3]{B};](/pictures/dewiki/99/c775bcae838bf0b5598c802b01db719e.png) .
.
Setzt man in der Gleichung
die beiden Ausdrücke in eckigen Klammern separat gleich null, erhält man eine quadratische Gleichung für A und B. Führt man die entsprechende Rechnung durch, ergeben sich die Cardanischen Formeln.
Analytische Bestimmung reeller Lösungen
Es seien alle Koeffizienten der Gleichung reell. Eine weitere Vereinfachung der Gleichung nach Entfernen des quadratischen Terms ergibt sich durch Skalieren der Variablen,
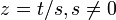 , und Multiplizieren der Gleichung mit s3,
, und Multiplizieren der Gleichung mit s3,- 0 = t3 + s2pt + s3q.
Ist p=0, so ist eine Lösung der Gleichung durch
![z=\sqrt[3]{-q}](/pictures/dewiki/56/84389741986daf39f3be9cec2491de1d.png) gegeben.
gegeben.Für
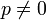 kann s so gewählt werden, dass
kann s so gewählt werden, dass 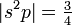 und
und 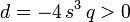 gleichzeitig gilt.
gleichzeitig gilt.Dann wird die Lösung des verbleibenden, klassisch "casus irreducibilis" genannten Falls mit trigonometrischen und hyperbolischen, also analytischen, als Potenzreihen auswertbaren Funktionen berechnet[1]. Es ergeben sich vier Fälle:
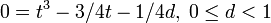 . Es gibt drei reelle Lösungen: Sie werden durch Koeffizientenvergleich mit der trigonometrischen Gleichung cos(3x) = 4cos3x − 3cosx = d gefunden; 3x = arccosd; t1 = cosx; t2 = cos(x + 120o), t3 = cos(x + 240o)
. Es gibt drei reelle Lösungen: Sie werden durch Koeffizientenvergleich mit der trigonometrischen Gleichung cos(3x) = 4cos3x − 3cosx = d gefunden; 3x = arccosd; t1 = cosx; t2 = cos(x + 120o), t3 = cos(x + 240o)
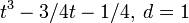 . Es gibt zwei reelle Lösungen: Sie können aus der Kurve y = t3 − 3 / 4t = 1 / 4 direkt entnommen werden: t1 = 1, t2 = t3 = − 1 / 2
. Es gibt zwei reelle Lösungen: Sie können aus der Kurve y = t3 − 3 / 4t = 1 / 4 direkt entnommen werden: t1 = 1, t2 = t3 = − 1 / 2
 . Es gibt eine reelle Lösung: Sie wird durch Koeffizientenvergleich mit der hyperbolischen Gleichung cosh(3x) = 4cosh3x − 3coshx = d gefunden; 3x = Arcoshd; t = coshx
. Es gibt eine reelle Lösung: Sie wird durch Koeffizientenvergleich mit der hyperbolischen Gleichung cosh(3x) = 4cosh3x − 3coshx = d gefunden; 3x = Arcoshd; t = coshx
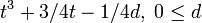 . Es gibt eine reelle Lösung: Auch hier wird die Lösung durch Koeffizientenvergleich mit einer hyperbolischen Gleichung gefunden: sinh(3x) = 4sinh3x + 3sinhx = d; 3x = Arsinhd; t = sinhx
. Es gibt eine reelle Lösung: Auch hier wird die Lösung durch Koeffizientenvergleich mit einer hyperbolischen Gleichung gefunden: sinh(3x) = 4sinh3x + 3sinhx = d; 3x = Arsinhd; t = sinhx
Siehe auch
Weblinks
Einzelnachweise
- ↑ Peter Gabriel: Matrizen, Geometrie, Lineare Algebra, Birkhäuser 1996, ISBN 3-7643-5376-7
Wikimedia Foundation.

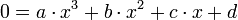
![0=z^3+pz+q
=\Big[A+B+q\Big]+\big(\sqrt[3]{A}+\sqrt[3]{B}\big)\Big[3\sqrt[3]{A}\sqrt[3]{B}+p\Big]](/pictures/dewiki/51/38443c61dca5cd55fdaafa19183c8846.png)