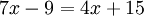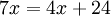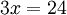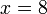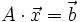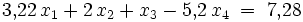- Gleichung ersten Grades
-
Die lineare Gleichung ist in der Mathematik ein einfacher, besonders häufig vorkommender Typ einer Bestimmungsgleichung. Eine Bestimmungsgleichung mit einer Unbekannten
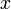 heißt linear, wenn sie auf folgende Form gebracht werden kann:
heißt linear, wenn sie auf folgende Form gebracht werden kann:Dabei stehen die Symbole
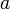 und
und 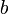 für konstante Zahlenwerte. Kennzeichnend ist für eine lineare Gleichung, dass die Unbekannte ausschließlich in der ersten Potenz steht, also nicht beispielsweise quadriert vorkommt (siehe quadratische Gleichung).
für konstante Zahlenwerte. Kennzeichnend ist für eine lineare Gleichung, dass die Unbekannte ausschließlich in der ersten Potenz steht, also nicht beispielsweise quadriert vorkommt (siehe quadratische Gleichung).Der Wert der Unbekannten
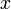 , mit dem die Gleichung erfüllt ist, kann aus der linearen Gleichung leicht bestimmt werden, indem auf beiden Seiten durch
, mit dem die Gleichung erfüllt ist, kann aus der linearen Gleichung leicht bestimmt werden, indem auf beiden Seiten durch 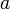 geteilt wird. Es ergibt sich danach für die Lösung:
geteilt wird. Es ergibt sich danach für die Lösung:Allerdings geht dies nur, wenn
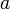 ungleich Null ist. Ist dies nicht der Fall, gibt es entweder gar keine oder unendlich viele Lösungen.
ungleich Null ist. Ist dies nicht der Fall, gibt es entweder gar keine oder unendlich viele Lösungen.Es gibt auch lineare Gleichungen mit mehreren Unbekannten und lineare Gleichungen, deren Unbekannte Vektoren oder andere mathematische Objekte sind.
Inhaltsverzeichnis
Lineare Gleichungen mit einer Unbekannten
Beispiel
Das folgende Beispiel zeigt, wie man eine einfache lineare Gleichung löst.
Zur Vereinfachung kann man zunächst auf beiden Seiten die Zahl 9 addieren.
Noch einfacher wird die Gleichung, wenn man auf beiden Seiten den Term (Rechenausdruck)
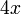 subtrahiert.
subtrahiert.Dividiert man diese Gleichung auf beiden Seiten durch 3, so bleibt auf der linken Seite nur noch die Unbekannte
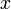 übrig.
übrig.Allgemeine lineare Gleichung
Allgemein im Bereich der reellen Zahlen lautet die lineare Gleichung:
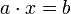 mit
mit 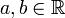
- Für
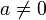 lässt sich die Lösung leicht angeben:
lässt sich die Lösung leicht angeben: 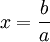
- Gilt
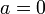 und
und  , so hat die Gleichung in
, so hat die Gleichung in  keine Lösung.
keine Lösung. - Gilt
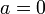 und
und 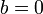 , so kann man für die Unbekannte jede Zahl
, so kann man für die Unbekannte jede Zahl 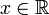 einsetzen.
einsetzen.
Entsprechendes ist auch richtig, wenn man als Grundmenge der Gleichung statt
 einen beliebigen Körper, zum Beispiel den Körper der komplexen Zahlen voraussetzt.
einen beliebigen Körper, zum Beispiel den Körper der komplexen Zahlen voraussetzt.Vektor als Unbekannte
Hauptartikel: Lineares Gleichungssystem
Sucht man eine Lösung einer linearen Gleichung in einer höheren Dimension, so erhält man ein lineares Gleichungssystem:
Hier ist A dann eine Matrix und x und b sind Vektoren. Da zu einer Matrix A nicht immer eine inverse Matrix A − 1 existiert, lässt sich auch obiges Lösungsverfahren nicht anwenden. Deshalb stehen zur Lösung linearer Gleichungssysteme eine Vielzahl von Lösungsverfahren zur Verfügung.
Lineare Gleichungen mit mehreren Unbekannten
Eine Gleichung, die mehrere Unbekannte enthält, ist linear, wenn sie in eine Form gebracht werden kann, in der die Unbekannten ausschließlich linear kombiniert sind. Eine lineare Gleichung mit n Unbekannten muss also – gegebenenfalls nach Umstellen – so aussehen:
Hierbei sind die Variablen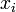 die Unbekannten und die Variablen
die Unbekannten und die Variablen 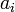 konstante Zahlen, die Koeffizienten der Gleichung. Auch
konstante Zahlen, die Koeffizienten der Gleichung. Auch 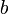 ist eine Konstante. Die Konstanten sind meist reelle oder komplexe Zahlen. Hier ein Beispiel für eine lineare Gleichung mit vier Unbekannten:
ist eine Konstante. Die Konstanten sind meist reelle oder komplexe Zahlen. Hier ein Beispiel für eine lineare Gleichung mit vier Unbekannten:Fasst man mehrere lineare Gleichungen mit mehreren Unbekannten zu einer Einheit zusammen, bekommt man ebenfalls ein lineares Gleichungssystem.
Siehe auch
Wikimedia Foundation.