Goldstone-Theorem

Das Goldstonetheorem ist ein Theorem der theoretischen Physik. Es besagt, dass beim spontanen Bruch einer Symmetrie des physikalischen Systems masselose Skalar-Teilchen, die Goldstonebosonen, auftreten.

Das Goldstonetheorem

Das Goldstonetheorem beschreibt die teilchenphysikalischen Auswirkungen von Symmetriebrechungen. Eine Symmetriebrechung tritt dann auf, wenn ein System aus einem symmetrischen Zustand in den Zustand niedrigster Energie übergeht (Vakuumzustand), der nicht mehr symmetrisch ist. Das Goldstonetheorem sagt aus, dass Modelle mit spontaner Symmetriebrechung masselose skalare Teilchen enthalten. Als Analogie kann ein Beispiel aus der Festkörperphysik betrachtet werden: bei ferromagnetischen Materialien sind die Gesetze, die sie beschreiben, invariant unter Drehungen im Raum. Oberhalb der Curie-Temperatur ist die Magnetisierung gleich null - also ebenfalls invariant unter räumlichen Drehungen. Unterhalb der Curie-Temperatur hat die Magnetisierung einen konstanten, von Null verschiedenen Wert und zeigt in eine bestimmte Richtung. Die Invarianz unter räumlichen Drehungen (also die Symmetrie) ist gebrochen. Die Goldstonebosonen sind in diesem Fall Magnonen.

Goldstonebosonen

Goldstonebosonen, auch Nambu-Goldstone-Bosonen genannt, sind masselose Elementarteilchen, die dann auftreten, wenn eine Symmetrie spontan gebrochen wird. Es wurde nach Jeffrey Goldstone benannt, der 1961 das Goldstonetheorem aufstellte, welches die Erzeugung dieser Teilchen postuliert. Goldstonebosonen (Bosonen sind Elementarteilchen mit ganzzahligen Spin) haben Spin 0, sind also Skalar-Teilchen. Die Zahl der Goldstone-Bosonen entspricht der Anzahl der Generatoren, die das Vakuum nicht invariant lassen.

In supersymmetrischen Theorien gibt es auch 'Goldstinos' (Goldstonefermionen).^[1] Im Fall globaler Symmetrie ist dies ein gewöhnliches Teilchen, bei lokaler Symmetrie verleiht es dem Graviton eine Masse (ähnlich wie das Higgs-Feld den W- und Z-Bosonen eine Masse gibt). Die bosonischen Superpartner der Goldstinos heißen 'Sgoldstinos'.^[2][3]

Beispiel: chirale Symmetriebrechung in der QCD

Ein Beispiel für Goldstone-Bosonen sind die Pionen: die Masse der beiden leichten u- und d-Quarks sind im Vergleich zur Massenskala der starken Wechselwirkung nahezu 0, so dass die starke Wechselwirkung eine näherungsweise globale 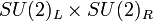$SU(2)_L \times SU(2)_R$-Symmetrie besitzt (eine sog. chirale Symmetrie, die links- und rechtshändige Felder unabhängig voneinander transformiert). D.h. sie ist invariant unter der Transformation

$\begin{pmatrix} u_L \\ d_L \end{pmatrix} \mapsto U \begin{pmatrix} u_L \\ d_L \end{pmatrix}, \begin{pmatrix} u_R \\ d_R \end{pmatrix} \mapsto V \begin{pmatrix} u_R \\ d_R \end{pmatrix}$

wobei U und V voneinder unabhängige SU(2)-Matrizen sind. Das QCD-Vakuum bricht diese Symmetrie spontan, im Teilchenspektrum beobachtet man nur eine SU(2), die links- und rechtshändige-Komponenten gleichzeitig dreht (d.h. die Matrizen U und V in obiger Transformation müssen identisch sein. Diese verbleibende SU(2)_{L + R}-Symmetrie ist als Isospin-Symmetrie bekannt). Die Pionen spielen die Rolle der Goldstonebosonen. Da u- und d-Quarks jedoch nicht exakt masselos sind (nur dann lassen sich links- und rechtshändige Quarkfelder unabhängig voneinander transformieren), ist die 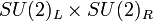$SU(2)_L \times SU(2)_R$-Symmetrie nicht nur spontan, sondern auch explizit gebrochen, so dass die Goldstonebosonen nicht exakt masselos sind, weshalb man auch von Pseudo-Goldstonebosonen spricht. Allerdings ist die Masse der Pionen sehr klein im Vergleich zur Masse von Proton oder Neutron.

Einzelnachweise und Fußnoten

1. ↑ Siehe auch englisches Wikipedia: Goldstone boson
2. ↑ DELPHI Collaboration: P. Abreu et al.: Search for the sgoldstino at √s from 189 to 202. In: CERN-EP/2000-110. 16.08.2000, S. 12 ([1]).  (Accepted by Phys.Lett.B)
3. ↑ Daniel M. Kaplan, Illinois Institute of Technology (IIT): GeVEvidence for the Sgoldstino in the Decay Σ⁺ → pμ⁺μ^– from the HyperCP Experiment. In: SUSY 2005, University of Durham. 18.07.2005, S. 25 ([2]). 

Weblinks

• Seminarvortrag zum Thema Symmetriebruch und Goldstonetheorem
• Goldstoneboson in der Astronomy Knowledge Data Base
• "A Goldstone Boson Primer" (engl.)

Literatur

• J. Goldstone: In: Il Nuovo Cimento. 19/1961, S. 154
• J. Goldstone, A. Salam, S. Weinberg: Broken Symmetries In: Physical Review. 127/3/1962, S. 965-970 ISSN 0031-899X

Siehe auch

• Symmetriebrechung
• Noethertheorem
• Higgs-Mechanismus