Algebraische Körpererweiterung
- Algebraische Körpererweiterung
-
In der Algebra heißt eine Körpererweiterung 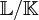 algebraisch, wenn jedes Element von
algebraisch, wenn jedes Element von 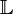 algebraisch über
algebraisch über  ist, d.h. wenn jedes Element von
ist, d.h. wenn jedes Element von 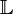 Nullstelle eines Polynoms mit Koeffizienten in
Nullstelle eines Polynoms mit Koeffizienten in  ist. Körpererweiterungen, die nicht algebraisch sind, also transzendente Elemente enthalten, heißen transzendent.
ist. Körpererweiterungen, die nicht algebraisch sind, also transzendente Elemente enthalten, heißen transzendent.
Zum Beispiel sind die Erweiterungen 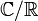 und
und 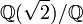 algebraisch, während
algebraisch, während 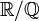 transzendent ist.
transzendent ist.
Ist 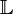 ein Oberkörper von
ein Oberkörper von  , dann kann man
, dann kann man 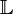 als
als  -Vektorraum auffassen und seine Dimension bestimmen. Diese Vektorraumdimension wird Grad der Körpererweiterung genannt. Je nachdem, ob dieser Grad endlich oder unendlich ist, teilt man Körpererweiterungen in endliche Erweiterungen und unendliche Erweiterungen ein. Jede transzendente Erweiterung ist unendlich; daraus folgt, dass jede endliche Erweiterung algebraisch ist.
-Vektorraum auffassen und seine Dimension bestimmen. Diese Vektorraumdimension wird Grad der Körpererweiterung genannt. Je nachdem, ob dieser Grad endlich oder unendlich ist, teilt man Körpererweiterungen in endliche Erweiterungen und unendliche Erweiterungen ein. Jede transzendente Erweiterung ist unendlich; daraus folgt, dass jede endliche Erweiterung algebraisch ist.
Es gibt aber auch unendliche algebraische Erweiterungen, zum Beispiel bilden die algebraischen Zahlen eine unendliche Erweiterung von  .
.
Ist a algebraisch über  , dann ist der Ring
, dann ist der Ring ![\mathbb{K}[a]](/pictures/dewiki/50/2dd8d6fd621060b35d3edcee13ad0689.png) aller Polynome in a über
aller Polynome in a über  sogar ein Körper.
sogar ein Körper. ![\mathbb{K}[a]](/pictures/dewiki/50/2dd8d6fd621060b35d3edcee13ad0689.png) ist eine endliche algebraische Erweiterung von
ist eine endliche algebraische Erweiterung von  , . Solche Erweiterungen, die durch Adjunktion eines einzigen Elements entstehen, heißen einfache Erweiterungen.
, . Solche Erweiterungen, die durch Adjunktion eines einzigen Elements entstehen, heißen einfache Erweiterungen.
Ein Körper, der keine echte algebraische Erweiterung besitzt, ist algebraisch abgeschlossen.
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
algebraische Gleichung — algebraische Gleichung, allgemein jede Gleichung der Form f (z1, z2,. .., zn) = 0, in der f ein Polynom, im weiteren Sinn eine ganzrationale Funktion von n … Universal-Lexikon
Körpererweiterung (Mathematik) — In der abstrakten Algebra ist ein Unterkörper eines Körpers L eine Teilmenge , die 0 und 1 enthält und mit den auf K eingeschränkten Verknüpfungen selbst ein Körper ist. L wird dann Oberkörper von K genannt. Das Paar L und K bezeichnet man als… … Deutsch Wikipedia
Körpererweiterung — In der abstrakten Algebra ist ein Unterkörper K eines Körpers L eine Teilmenge , die 0 und 1 enthält und mit den auf K eingeschränkten Verknüpfungen selbst ein Körper ist. L wird dann Oberkörper von K genannt. Das Paar L und K bezeichnet man als… … Deutsch Wikipedia
Algebraische Erweiterung — In der Algebra heißt eine Körpererweiterung algebraisch, wenn jedes Element von algebraisch über ist, d.h. wenn jedes Element von Nullstelle eines Polynoms mit Koeffizienten in ist. Körpererweiterungen, die nicht algebraisch sind, also… … Deutsch Wikipedia
Algebraische Unabhängigkeit — In der abstrakten Algebra ist die algebraische Unabhängigkeit eine Eigenschaft von Elementen einer transzendenten Körpererweiterung, welche besagt, dass diese Elemente keine nichttriviale Polynomgleichung mit Koeffizienten im Grundkörper erfüllen … Deutsch Wikipedia
Verzweigte Körpererweiterung — Verzweigung ist ein mathematischer Begriff, der die Gebiete Algebra, algebraische Geometrie und komplexe Analysis miteinander verbindet. Inhaltsverzeichnis 1 Namengebendes Beispiel 2 Verzweigung im Kontext von Erweiterungen bewerteter Körper 2.1… … Deutsch Wikipedia
Diskriminante (algebraische Zahlentheorie) — In der Algebraischen Zahlentheorie bezeichnet die Diskriminante ein Hauptideal in einem Ganzheitsring, welches eine zahlentheoretische Aussage über die Körpererweiterung zweier Zahlkörper macht. Inhaltsverzeichnis 1 Definition 2 Eigenschaften und … Deutsch Wikipedia
Ordnung (algebraische Zahlentheorie) — In der algebraischen Zahlentheorie ist eine Ordnung des Zahlkörpers K ein Unterring von K, der (via Multiplikation) als Endomorphismenring auf bestimmten Untergruppen von K, den Gittern operiert, zugleich ist die Ordnung selbst ein spezielles… … Deutsch Wikipedia
Endliche Galoiserweiterung — In der abstrakten Algebra ist ein Unterkörper eines Körpers L eine Teilmenge , die 0 und 1 enthält und mit den auf K eingeschränkten Verknüpfungen selbst ein Körper ist. L wird dann Oberkörper von K genannt. Das Paar L und K bezeichnet man als… … Deutsch Wikipedia
Erweiterungskörper — In der abstrakten Algebra ist ein Unterkörper eines Körpers L eine Teilmenge , die 0 und 1 enthält und mit den auf K eingeschränkten Verknüpfungen selbst ein Körper ist. L wird dann Oberkörper von K genannt. Das Paar L und K bezeichnet man als… … Deutsch Wikipedia
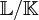 algebraisch, wenn jedes Element von
algebraisch, wenn jedes Element von 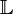 algebraisch über
algebraisch über  ist, d.h. wenn jedes Element von
ist, d.h. wenn jedes Element von 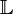 Nullstelle eines Polynoms mit Koeffizienten in
Nullstelle eines Polynoms mit Koeffizienten in  ist. Körpererweiterungen, die nicht algebraisch sind, also transzendente Elemente enthalten, heißen transzendent.
ist. Körpererweiterungen, die nicht algebraisch sind, also transzendente Elemente enthalten, heißen transzendent.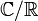 und
und 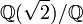 algebraisch, während
algebraisch, während 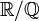 transzendent ist.
transzendent ist.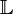 ein Oberkörper von
ein Oberkörper von  , dann kann man
, dann kann man 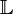 als
als  -Vektorraum auffassen und seine Dimension bestimmen. Diese Vektorraumdimension wird Grad der Körpererweiterung genannt. Je nachdem, ob dieser Grad endlich oder unendlich ist, teilt man Körpererweiterungen in endliche Erweiterungen und unendliche Erweiterungen ein. Jede transzendente Erweiterung ist unendlich; daraus folgt, dass jede endliche Erweiterung algebraisch ist.
-Vektorraum auffassen und seine Dimension bestimmen. Diese Vektorraumdimension wird Grad der Körpererweiterung genannt. Je nachdem, ob dieser Grad endlich oder unendlich ist, teilt man Körpererweiterungen in endliche Erweiterungen und unendliche Erweiterungen ein. Jede transzendente Erweiterung ist unendlich; daraus folgt, dass jede endliche Erweiterung algebraisch ist. .
. , dann ist der Ring
, dann ist der Ring ![\mathbb{K}[a]](/pictures/dewiki/50/2dd8d6fd621060b35d3edcee13ad0689.png) aller Polynome in a über
aller Polynome in a über  sogar ein Körper.
sogar ein Körper. ![\mathbb{K}[a]](/pictures/dewiki/50/2dd8d6fd621060b35d3edcee13ad0689.png) ist eine endliche algebraische Erweiterung von
ist eine endliche algebraische Erweiterung von  , . Solche Erweiterungen, die durch Adjunktion eines einzigen Elements entstehen, heißen einfache Erweiterungen.
, . Solche Erweiterungen, die durch Adjunktion eines einzigen Elements entstehen, heißen einfache Erweiterungen.