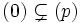Hauptidealsatz

Die Dimension oder genauer Krulldimension (nach Wolfgang Krull), auch Chevalleydimension (nach Claude Chevalley), eines kommutativen Ringes mit Einselement ist die anschauliche Dimension der ihm in der algebraischen Geometrie zugeordneten Varietät oder allgemeiner des zugehörigen Schemas.

Dieser Artikel beschäftigt sich mit kommutativer Algebra. Insbesondere sind alle betrachteten Ringe kommutativ und haben ein Einselement. Für weitere Details siehe Kommutative Algebra.

Definition

Die Höhe ht P eines Primideales P ist die maximale Länge einer aufsteigenden Kette von Primidealen

$P_0\subsetneq P_1\subsetneq\ldots\subsetneq P_n=P;$

die Höhe ist dann n. Gibt es keine maximale Länge, hat das Primideal unendliche Höhe.

Die Dimension dim A eines Ringes A ist das Supremum der Höhen seiner Primideale.

Eigenschaften

• In einem noetherschen Ring hat jedes Primideal endliche Höhe, insbesondere sind noethersche lokale Ringe endlichdimensional. Es gibt aber auch noethersche Ringe unendlicher Dimension.
• Die Höhe eines Primideals ist gleich der Kodimension der entsprechenden abgeschlossenen Teilmenge des Spektrums des Ringes.
• Krulls Hauptidealsatz besagt, dass die Höhe von Primidealen, die minimal über einem Hauptideal liegen (d.h. es enthalten und bezüglich dieser Eigenschaft minimal sind), höchstens 1 sein kann. Allgemeiner ist die Höhe von Primidealen, die minimal über einem Ideal liegen, das von r Elementen erzeugt werden kann, höchstens r.

Beispiele

• dim Z = 1. Maximale aufsteigende Ketten von Primidealen haben die Form

$(0) \subsetneq (p)$

für Primzahlen p.

• Ein Integritätsbereich ist genau dann eindimensional, wenn jedes von Null verschiedene Primideal maximal ist. Für weitere Beispiele eindimensionaler Integritätsbereiche siehe Dedekindring.
• Körper sind nulldimensional, allgemeiner alle artinschen Ringe.
• Die Formel dim A[X] = dim A + 1 gilt für noethersche Ringe A; insbesondere hat der affine Koordinatenring des n-dimensionalen affinen Raums über einem Körper Dimension n.