Hebbar

Eine Singularität bezeichnet in der Mathematik einen Punkt an dem ein mathematisches Objekt nicht definiert ist oder an der eine sonst zutreffende Eigenschaft nicht vorhanden ist. Beispiele von Mengen mit singulären Punkten sind:

• Ein Intervall, auf welchem mit Ausnahme endlich vieler Stellen eine Funktion definiert ist.
• Ein Intervall, auf welchem eine Funktion definiert ist, die mit Ausnahme endlich vieler Stellen stetig (stetig differenzierbar, …) ist.
• Eine offene Menge (z. B. eine Kreisscheibe) in der komplexen Zahlenebene, auf der, mit Ausnahme endlich vieler Punkte, eine komplexwertige Funktion definiert und holomorph ist.
• Sei 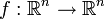$f : \R^n \to \R^n$ die reelle Funktion, deren Jacobi-Matrix auf einer echten Teilmenge ihres Definitionsbereichs nicht invertierbar ist.

In der Nähe einer Singularität zeigt das betrachtete mathematische Objekt oft ungewöhnliches Verhalten z. B. Oszillationen oder unbeschränktes Wachstum. An diesen Stellen versagen die für das Objekt üblichen Methoden, numerische Methoden weisen oft in der Nähe von Singularitäten große Rundungsfehler auf.

Je nach Herkunft kann man Singularitäten weitergehend kategorisieren. Eine besonders klare Kategorisierung von Singularitäten findet man in der Funktionentheorie. Dort sind isolierte Singularitäten holomorpher Funktionen exakt in hebbare Singularitäten, Pole und wesentliche Singularitäten unterteilt. Für reelle Funktionen gibt es diese Typen ebenfalls, allerdings schöpfen sie nicht alle Möglichkeiten aus.

In der Schulmathematik sind insbesondere stetig behebbare Definitionslücken und Polstellen reeller Funktionen interessant.

Singularitäten komplexer Funktionen

Es sei 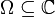$\Omega \subseteq \mathbb C$ eine offene Teilmenge, 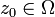$z_0 \in \Omega$, ferner sei 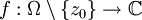$f: \Omega \setminus \{z_0\} \to \mathbb C$ eine holomorphe komplexwertige Funktion.

Dann heißt z₀ isolierte Singularität von f.

Jede isolierte Singularität gehört einer der folgenden drei Klassen an:

• z₀ heißt hebbare Singularität, wenn f auf Ω holomorph fortsetzbar ist. Nach dem riemannschen Hebbarkeitssatz ist dies z. B. dann der Fall, wenn f in einer Umgebung von z₀ beschränkt ist.
• z₀ heißt Polstelle oder Pol, wenn z₀ keine hebbare Singularität ist und es eine natürliche Zahl k gibt, sodass 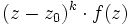$(z-z_0)^k\cdot f(z)$ eine hebbare Singularität bei z₀ hat. Ist das k minimal gewählt, dann sagt man, f habe in z₀ einen Pol k-ter Ordnung.
• Andernfalls heißt z₀ eine wesentliche Singularität von f.

Hebbare Singularitäten und Polstellen werden auch unter dem Begriff außerwesentliche Singularität zusammengefasst.

Der Typ der Singularität lässt sich auch an der Laurentreihe

$\sum_{n=-\infty}^\infty a_n(z-z_0)^n$

von f in z₀ ablesen:

• Eine hebbare Singularität liegt genau dann vor, wenn der Hauptteil verschwindet, d. h. a_n = 0 für alle negativen ganzen Zahlen n.
• Ein Pol k-ter Ordnung liegt genau dann vor, wenn der Hauptteil nach k Gliedern abbricht, d. h. a_n = 0 für alle n < − k.
• Eine wesentliche Singularität liegt genau dann vor, wenn unendlich viele Glieder mit negativem Exponenten nicht verschwinden.

Aussagen über die Eigenschaften holomorpher Funktionen an wesentlichen Singularitäten machen der Große Satz von Picard und als einfacherer Spezialfall davon der Satz von Casorati-Weierstraß.

Beispiele

Plot der Funktion exp(1 / z). Sie hat im Nullpunkt eine wesentliche Singularität (Bildmitte). Der Farbton entspricht dem komplexen Argument des Funktionswertes, während die Helligkeit seinen Betrag darstellt. Hier sieht man, dass sich die wesentliche Singularität unterschiedlich verhält, je nachdem, wie man sich ihr nähert (im Gegensatz dazu wäre ein Pol gleichmäßig weiß).

Es sei 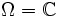$\Omega=\mathbb C$ und z₀ = 0.

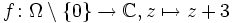• $f\colon \Omega \setminus \{0\}\to\mathbb C,z\mapsto z+3$ kann durch f(0) = 3 stetig auf Ω fortgesetzt werden, also hat f bei 0 eine hebbare Singularität.
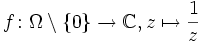• $f\colon \Omega\setminus \{0\}\to\mathbb C,z\mapsto \frac{1}{z}$ hat bei 0 einen Pol erster Ordnung, weil 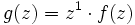$g(z)=z^1\cdot f(z)$ durch g(0) = 1 stetig auf Ω fortgesetzt werden kann.
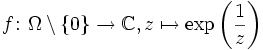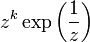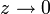• $f\colon \Omega\setminus \{0\}\to\mathbb C,z\mapsto\exp\left(\frac{1}{z}\right)$ hat bei 0 eine wesentliche Singularität, weil $z^k \exp\left(\frac{1}{z}\right)$ für $z\to 0$ für festes 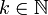$k\in\mathbb N$ stets unbeschränkt ist bzw. weil in der Laurentreihe um z₀ unendlich viele Glieder des Hauptteils nicht verschwinden, denn es gilt $f(z)=\sum\limits_{n=0}^{\infty}\frac{1}{n!\,z^n}$.

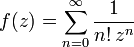Singularitäten algebraischer Varietäten

Ein Punkt x einer algebraischen Varietät oder allgemeiner eines Schemas heißt singulär oder eine Singularität, wenn der zugehörige lokale Ring nicht regulär ist. Für abgeschlossene Punkte algebraischer Varietäten ist dies äquivalent dazu, dass die Dimension des Zariski-Tangentialraumes größer als die Dimension der Varietät ist.

Andere Singularitäten

• Attraktoren
• singuläre Matrizen
• Regulärer Wert