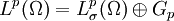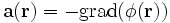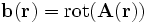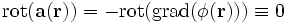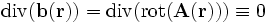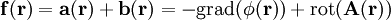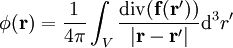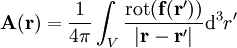Helmholtzscher Zerlegungssatz

Das Helmholtz-Theorem (auch Helmholtz-Zerlegung) ist nach Hermann von Helmholtz benannt. Es besagt, dass für gewisse Gebiete 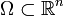$\Omega\subset\R^n$ der L^p-Raum als direkte Summe von divergenzfreien Funktionen und Gradientenfeldern geschrieben werden kann.

Definition

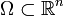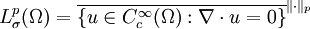Für ein Gebiet $\Omega\subset\R^n$ wird $L^p_\sigma(\Omega)=\overline{\{u\in C_c^\infty(\Omega): \nabla\cdot u=0\}}^{\|\cdot\|_p}$ der Raum der divergenzfreien Funktionen genannt, wobei 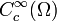$C_c^\infty(\Omega)$ der Raum der Testfunktionen ist und 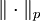$\|\cdot\|_p$ die p-Norm bezeichnet. Die Zerlegung

$L^p(\Omega)=L^p_\sigma(\Omega) \oplus G_p$

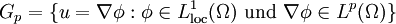mit $G_p=\{u=\nabla\phi: \phi\in L^1_\text{loc}(\Omega) \ \text{und}\ \nabla\phi \in L^p(\Omega)\}$ wird Helmholtz-Zerlegung genannt, insofern die Zerlegung existiert. In diesem Fall gibt es eine Projektion P mit 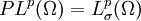$PL^p(\Omega)=L^p_\sigma(\Omega)$, die sog. Helmholtz-Projektion.

Ist Ω der Halbraum, ein beschränktes Gebiet mit C²-Rand oder ein Außenraum mit C²-Rand, so existiert die Zerlegung. Für p = 2 existiert die Zerlegung für beliebige Gebiete mit C²-Rand.^[1]

Hat Ω einen C¹-Rand, gilt 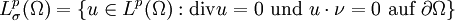$L^p_\sigma(\Omega)=\{u\in L^p(\Omega): \operatorname{div} u=0 \ \text{und}\ u\cdot \nu=0 \ \text{auf}\ \partial\Omega\}$, wobei ν die äußere Normale ist.

Mathematische Anwendung

In der Lösbarkeitstheorie der Navier-Stokes-Gleichungen spielt die Helmholtz-Projektion eine wichtige Rolle. Wird die Helmholtz-Projektion auf die linearisierte inkompressiblen Navier-Stokes-Gleichungen angewandt, erhält man die Stokes-Gleichung

u_t − PΔu = f

für 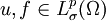$u,f\in L^p_\sigma(\Omega)$. Gab es zuvor zwei Unbekannte, nämlich u und p, gibt es jetzt nur noch eine Unbekannte. Beide Gleichungen, die Stokes- und die linearisierte Gleichung, sind jedoch äquivalent.

Der Operator PΔ wird Stokes-Operator genannt.

Physikalische Betrachtung

Das Helmholtz-Theorem besagt, dass es möglich ist, ein (fast) beliebiges Vektorfeld 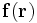$\mathbf{f}(\mathbf{r})$ als eine Superposition eines rotationsfreien Feldes 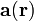$\mathbf{a}(\mathbf{r})$ und eines divergenzfreien Feldes 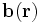$\mathbf{b}(\mathbf{r})$ darzustellen. Ein rotationsfreies Feld lässt sich jedoch wiederum durch ein skalares Potential 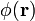$\phi(\mathbf{r})$ darstellen, ein divergenzfreies Feld durch ein Vektorpotential $\mathbf{A}(\mathbf{r})$.

$\mathbf{a}(\mathbf{r}) = -\operatorname{grad}(\phi(\mathbf{r}))$

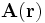und

$\mathbf{b}(\mathbf{r}) = \operatorname{rot}(\mathbf{A}(\mathbf{r}))$

dann folgt

$\operatorname{rot}(\mathbf{a}(\mathbf{r})) = -\operatorname{rot}(\operatorname{grad}(\phi(\mathbf{r})))\equiv 0$

und

$\operatorname{div}(\mathbf{b}(\mathbf{r})) = \operatorname{div}(\operatorname{rot}(\mathbf{A}(\mathbf{r})))\equiv 0$

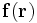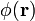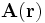Es ist also möglich das Vektorfeld $\mathbf{f}(\mathbf{r})$ durch Superposition (Addition) zweier unterschiedlicher Potentiale $\phi(\mathbf{r})$ und $\mathbf{A}(\mathbf{r})$ auszudrücken (das Helmholtz-Theorem).

$\mathbf{f}(\mathbf{r}) = \mathbf{a}(\mathbf{r}) + \mathbf{b}(\mathbf{r}) = -\operatorname{grad}(\phi(\mathbf{r})) + \operatorname{rot}(\mathbf{A}(\mathbf{r}))$

Die beiden einander ergänzenden Potentiale lassen sich durch die folgenden Integrale aus dem Feld 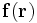$\mathbf{f}(\mathbf{r})$ gewinnen:

$\phi(\mathbf{r}) = \frac{1}{4\pi}\int_V \frac{\operatorname{div}(\mathbf{f}(\mathbf{r}'))}{|\mathbf{r}-\mathbf{r}'|}\mathrm{d}^3r'$

$\mathbf{A}(\mathbf{r}) = \frac{1}{4\pi}\int_V \frac{\operatorname{rot}(\mathbf{f}(\mathbf{r}'))}{|\mathbf{r}-\mathbf{r}'|} \mathrm{d}^3r'$

Wobei V das die Felder enthaltende Volumen ist.

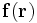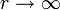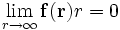Die mathematische Voraussetzung für die Anwendung des Helmholtzschen Theorems ist neben der Differenzierbarkeit des Vektorfelds $\mathbf{f}(\mathbf{r})$, dass es für $r \to \infty$ schneller als $\frac{1}{r}$ gegen 0 geht, also $\lim_{r \to \infty} \mathbf{f}(\mathbf{r}) r = 0$. Ansonsten divergieren die obigen Integrale, lassen sich also nicht mehr berechnen.

Dieses Theorem ist besonders in der Elektrodynamik von Interesse, da sich mit seiner Hilfe die Maxwell-Gleichungen im Potentialbild schreiben und einfacher lösen lassen. Für alle physikalisch relevanten Probleme sind dabei die mathematischen Voraussetzungen erfüllt.

Quellen

1. ↑ G. P. Galdi, An introduction to the mathematical theory of the Navier-Stokes equations. Vol. I, Springer Tracts in Natural Philosophy, vol. 38, Springer-Verlag, New York, 1994, ISBN 0-387-94172-X