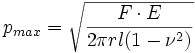- Hertz'sche Pressung
-
Unter der Hertzschen Pressung versteht man die größte Spannung, die in der Mitte der Berührfläche zweier elastischer Körper herrscht.
Werden zwei elastische Körper mit gewölbter Oberfläche (Zylinder oder Kugeln) gegeneinander gepresst, dann berühren sie sich im idealisiertem Fall nur linien- oder punktförmig. Durch die Elastizität entsteht aber im realen Fall an der Berührstelle eine Abplattung und eine Berührungsfläche. Auf der Berührungsfläche entsteht in beiden Körpern eine charakteristische Spannungsverteilung (Flächenpressung), wobei die Spannung stets in der Mitte am höchsten ist.
Berühren sich zwei Kugeln, eine Kugel und eine Ebene oder zwei gekreuzte Zylinder, so entsteht eine Berührellipse. Bei Berührung zweier paralleler Zylinder oder eines Zylinders mit einer Ebene entsteht eine linienförmige Berührungsfläche; man spricht hier auch von Walzenpressung.
Nach den Theorien des deutschen Physikers Heinrich Hertz können Größe und Form der Berührflächen sowie die Höhe und Verteilung der mechanischen Spannungen unter den Berührflächen berechnet werden. Nach Hertz wird die höchste Spannung, die in der Mitte der Berührfläche herrscht, auch Hertzsche Pressung genannt.
Die Höhe der Hertzschen Pressung hängt ab von der Kraft, mit der die beiden Körper aufeinander gepresst werden, von ihren Krümmungsradien und von ihren Elastizitätsmoduln.
Inhaltsverzeichnis
Berechnung
Voraussetzungen für die Berechnung der Flächenpressung nach den Hertzschen Gleichungen sind
- linear-elastische, homogene und isotrope Werkstoffe
- Kontaktfläche eben und klein (gegenüber den Abmessungen der Körper)
- Reibungsfreiheit, keine Schubspannungen in der Kontaktfläche
- die Körper können als elastische Halbräume betrachtet werden
Allgemein
Die Hertzsche Pressung bei Kontakt gekrümmter Oberflächen berechnet sich nach folgender Gleichung:
wobei gilt:
F -- Kraft zwischen den Körpern
E -- E-Modul
Es gilt:

ν1,2 -- Poissonzahl (auch: Querkontraktionszahl) Körper 1, Körper 2E1,2 -- E-Modul der Werkstoffe Körper 1, Körper 2
ξ,η -- Beiwerte nach Hertz für die Berührung gekrümmter Oberflächenk -- Krümmung
Punktberührung Kugel - Kugel
Für den einfachen Berührungsfall Kugel - Kugel (oder Ebene) gilt:
und
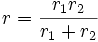
sowie
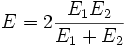
mit
r1,2 -- Kugelradien Kugel 1, Kugel 2; Sonderfall Ebene:
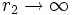 und damit r = r1
und damit r = r1Linienberührung Zylinder - Zylinder
Für den einfachen Berührungsfall Zylinder - Zylinder (oder Ebene) gilt:
mit
l -- Berührungslänge der Zylinder
F -- als Linienlast über die Berührungslänge wirkende Kraft
r1,2 -- Zylinderradien Zylinder 1, Zylinder 2; Sonderfall Ebene:
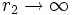 und damit r = r1
und damit r = r1Siehe auch
Weblinks
Wikimedia Foundation.


![p_{max} = \frac{1} {\xi \cdot \eta} \cdot \sqrt[3]{\frac{3F \cdot E^2 \cdot (\sum k)^2}{{{8\pi}^3 (1-{\nu}^2)^2}} }](/pictures/dewiki/51/313ea6cd3c355589152728e37b6698a4.png)
![p_{max} = \frac{1} {\pi} \cdot \sqrt[3]{\frac{1,5 \cdot F E^2}{{{r}^2 (1-{\nu}^2)^2}} }](/pictures/dewiki/56/8710439e82f8f4fe53cd8f7333220bad.png)