2-Mannigfaltigkeit

Als Fläche bezeichnet man in den mathematischen Teilgebieten der Differentialgeometrie und Topologie eine 2-dimensionale Mannigfaltigkeit. Beispiele im 3-dimensionalen Raum gewinnt man, wenn man die Oberflächen von Vollkörpern betrachtet.

Definition

Flächen in der Topologie

In der Topologie ist eine Fläche eine topologische 2-dimensionale Mannigfaltigkeit. Man kann sie deshalb wie folgt definieren:

Eine Fläche ist ein Hausdorffraum, der das zweite Abzählbarkeitsaxiom erfüllt und in dem jeder Punkt eine zur offenen Kreisscheibe 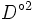$D^{\circ2}$ oder zur Halbebene 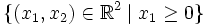$\lbrace (x_1,x_2) \in \mathbb R^2 \mid x_1 \geq 0 \rbrace$ homöomorphe Umgebung besitzt.

Eine alternative Definition, die auf die Fallunterscheidung verzichtet lautet:

Eine Fläche ist ein Hausdorffraum, der das zweite Abzählbarkeitsaxiom erfüllt und in dem jeder Punkt eine zur geschlossenen Kreisscheibe D² homöomorphe Umgebung besitzt.

Diejenigen Punkte, die eine zur offenen Kreisscheibe homöomorphe Umgebung besitzen, bezeichnet man als innere Punkte der Fläche und die anderen als Randpunkte. Die Menge der inneren Punkte bildet das Innere 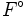$F^\circ$ der Fläche, während die Menge der Randpunkte den Rand 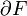$\partial F$ der Fläche bildet.

Hat eine Fläche keine Randpunkte, so spricht man von einer unberandeten Fläche oder Fläche ohne Rand. Andernfalls nennt man die Fläche berandet oder Fläche mit Rand.

Für unberandete Flächen verkürzt sich die obige Definition:

Eine unberandete Fläche ist ein Hausdorffraum, der das zweite Abzählbarkeitsaxiom erfüllt und in dem jeder Punkt eine zur offenen Kreisscheibe 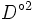$D^{\circ2}$ homöomorphe Umgebung besitzt.

Flächen in der Differentialgeometrie

In der Differentialgeometrie ist eine Fläche eine differenzierbare 2-dimensionale Mannigfaltigkeit. Für die genaue Definition siehe differenzierbare Mannigfaltigkeit.

Mathematische Attribute für unberandete Flächen

geschlossen

Eine Fläche ohne Rand heißt geschlossen, wenn sie kompakt ist.

offen

Eine unberandete Fläche heißt offen, wenn sie nicht kompakt ist.

Beispiele

• Die bekannten Standardflächen in der Ebene, etwa Dreieck(-sfläche), Kreisscheibe, Halbebene; diese sind berandet oder unberandet im Sinne der obigen Definition je nachdem ob man die Randlinie hinzuzählt oder nicht.
• Oberflächen von Vollkörpern, etwa Polyeder, Kugel, Zylinder, Kegel, ebenso geeignete Teile hiervon, etwa nur der Mantel eines Zylinders.
• Das Möbiusband ist eine nicht orientierte Fläche.
• Die Kleinsche Flasche ist eine geschlossene Fläche, aber keine Oberfläche eines Vollkörpers und lässt sich noch nicht einmal in den dreidimensionalen Raum einbetten.

Siehe auch

• Geschlecht (Fläche)
• Riemannsche Fläche
• Abwickelbare Fläche
• Euler-Charakteristik
• Eulerscher Polyedersatz
• Geodäte
• Fundamentalpolygon
• Klassifikationssatz für 2-Mannigfaltigkeiten

Literatur

• Ralph Stöcker, Heiner Zieschang: Algebraische Topologie. Teubner, Stuttgart 1988, ISBN 3-519-02226-5
• William S. Massey: Algebraic Topology: An Introduction. 1. Auflage. Springer, Berlin 1967, ISBN 3-540-90271-6