Houghtransformation

Houghtransformation

Die Hough-Transformation (Sprechweise [hʌf]) ist ein robustes globales Verfahren zur Erkennung von Geraden, Kreisen oder beliebigen anderen parametrisierbaren geometrischen Figuren in einem binären Gradientenbild, also einem schwarz/weiß Bild, nach einer Kantenerkennung. Das Verfahren wurde 1962 von Paul V. C. Hough unter dem Namen „Method and Means for Recognizing Complex Patterns“ patentiert.

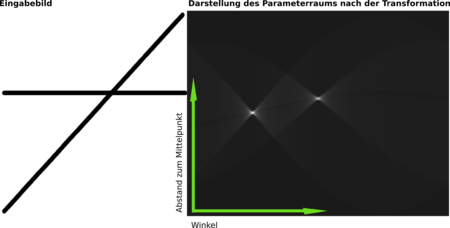
Zur Erkennung von geometrischen Objekten wird ein Dualraum erschaffen (speziell: Parameterraum, Hough-Raum), in den für jeden Punkt im Bild, der auf einer Kante liegt, alle möglichen Parameter der zu findenden Figur im Dualraum eingetragen werden. Jeder Punkt im Dualraum entspricht damit einem geometrischen Objekt im Bildraum. Bei der Gerade kann das z. B. die Steigung und der y-Achsen-Abschnitt sein, beim Kreis der Mittelpunkt und Radius. Danach wertet man den Dualraum aus, indem man nach Häufungen sucht, die dann der gesuchten Figur entsprechen.

Inhaltsverzeichnis

Geradenerkennung mittels Hough-Transformation

Darstellung einer Hough-Transformation eines Pixelbildes mit zwei Linien zu einem Raum aus Winkel und Abstand zum Bildmittelpunkt. Die beiden hellen Punkte im Ergebnisraum sind die Schnittpunkte der Kurven der beiden Eingabelinien und damit die gesuchten Häufungspunkte.

Bei der Geradenerkennung mittels der Hough-Transformation muss man zuerst geeignete Parameter für eine Gerade finden. Steigung und y-Achsen-Abschnitt eignen sich nur bedingt, da zur y-Achse parallele Geraden eine unendliche Steigung haben und daher im (für die Berechnung zwangsläufig) endlichen Parameterraum nicht mehr abgebildet werden können. Dieses Problem kann man umgehen, wenn man eine zweite Hough-Transformation auf dem um 90° gedrehten Bildraum durchführt, was aber recht umständlich ist. In der neueren Literatur überwiegt daher der Ansatz, Geraden durch ihre Hessesche Normalform zu repräsentieren. Als Parameter wählt man den Winkel α und den (euklidischen) Abstand d, wobei α der Winkel der Normalen der Gerade zur x-Achse und d der Abstand vom Ursprung zur Geraden ist.

Damit haben wir die Parametergleichung 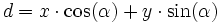d=x\cdot\cos(\alpha)+y\cdot\sin(\alpha) mit der wir für alle Punkte auf Kanten im Bild die entsprechende Kurve im Dualraum einzeichnen. Der nächste Schritt besteht in der Analyse des Dualraums, bei der man nach Häufungspunkten sucht. Diese Häufungspunkte im Dualraum repräsentieren mögliche Geraden im Bildraum.

Aufgrund der Unabhängigkeit der einzelnen Zellen des Parameterraumes zueinander bei der Berechnung der Häufungspunkte, ist die Hough-Transformation leicht parallelisierbar.

Einfacher Algorithmus

Ein einfacher Algorithmus um eine Hough-Akkumulation durchzuführen könnte etwa so aussehen:

houghRaum[0...π][0...n]:= 0
foreach pixel_auf_kante do
   for α:=0 to π do
      d:= pixel_auf_kantex * cos(α) + pixel_auf_kantey * sin(α)
      houghRaum[α][d]++
   end
end

Das Resultat der Akkumulation ist ein zweidimensionales Array, welches für die Häufigkeit des Auftretens für jede Kombination aus α und d enthält. Weil die Geraden nicht gerichtet sind, muss nur der Bereich von 0 bis π ausgewertet werden, da sich danach die Geraden mit den bereits berechneten decken. In der Praxis wird häufig die Bildmitte als Koordinatenursprung verwendet.

Hough-Transformation für Kreise und generalisierte Hough-Transformation

Wie oben erwähnt kann die Hough-Transformation – in abgewandelter Weise – nicht nur für das Detektieren von Geraden, sondern z. B. auch von Kreisen eingesetzt werden. Ausgehend vom Kantenbild wird jedes Kantenpixel als von Kreisen eines bestimmten Radius erzeugt angesehen. Die Transformation in den Hough-Raum funktioniert so, dass man im Akkumulator alle Kreismittelpunkte einträgt, die zu diesem Kantenpixel führen könnten (jedes Akkumulatormittelpunktpixel um 1 erhöhen). Wenn nun die Punkte im Kantenbild einen Kreis repräsentieren, ist in der Akkumulatormatrix ein besonders hoher Wert an der dazugehörigen Stelle des Kreismittelpunkts eingetragen, da dort sehr viele Kantenpixel des Kreises für den Mittelpunkt abgestimmt haben. Die Maxima im Hough-Raum repräsentieren also die Kreismittelpunkte.

Den ersten zwei Dimensionen des Hough-Raums entsprechen in diesem Fall denen des Bildraums, da die (x,y)-Koordinaten in beiden Fällen die Lage des Kreismittelpunktes beschreiben. Zusätzlich dazu ist laut der Kreisgleichung x2 + y2 = r2 der Radius r der 3. Parameter, der beachtet werden muss. Man spricht bei Kreisen daher von einem 3-dimensionalen Hough-Raum (xc, yc, r). Die Wertegrenzen für den Radius müssen fest vorgegeben werden (z. B. mittels a priori-Wissen).

Für Ellipsen und jede andere, durch eine parametrische Gleichung darstellbare Form, kann dieses Verfahren ebenfalls angewendet werden. Jedoch steigt die Dimension des Hough-Raums mit der Variablenzahl (bei Ellipsen: 5), was den Rechenaufwand deutlich steigert.

Es ist ebenfalls möglich, eine nicht durch parametrische Repräsentation darstellbare Struktur zu finden. Dieses Verfahren wird generalisierte Hough-Transformation (GHT) genannt. So können beliebige Formen in einem Bild gefunden werden. Das Prinzip hierbei ist, dass man eine formabhängige Lookup-Tabelle errechnet. In dieser sind die möglichen Vektoren zu einem Referenzpunkt den unterschiedlichen Gradientenrichtungen zugeordnet. Durch einige Umformungen der Tabelle kann man auch rotierte bzw. skalierte Versionen der gesuchten Formen finden, was zu einer hohen Robustheit führt. Mittels der Lookup-Tabelle kann man nun das Kantenbild in den Hough-Raum überführen; Maxima stellen die gefundenen Referenzpunkte dar.

Nachteile der Hough-Transformation

  • Die Hough-Transformation ist eine Art „Brute-Force-Ansatz“ und damit sehr rechenaufwändig.

In ihrer ursprünglichen Form ist die Hough-Transformation daher selbst in einem Parallelrechner z. B. nicht zur Analyse von Videosequenzen in Echtzeit geeignet, wie sie zur Erkennung von Fahrbahnmarkierungen beim autonomen Fahren notwendig ist. Es gibt jedoch eine kaum überschaubare Zahl von Weiterentwicklungen der Hough-Transformation, häufig „Fast Hough Transform“ benannt, die sich dieses Problems annehmen (siehe z. B. Fast Hough Transform).

  • Der Speicherbedarf des klassischen Ansatzes ist sehr groß. Auch diese Eigenschaft wurde in diversen wissenschaftlichen Publikationen verbessert.
  • Bei der Hough-Transformation werden statt der gewünschten Geraden oftmals viele gleichartige Geraden erkannt. Dieses Phänomen liegt im diskreten Bildraum begründet, in dem sich viele mögliche Gerade die gleichen Pixel teilen – was dazu führt, dass sich im Parameterraum keine Häufungspunkte sondern (im 2D-Fall bei der Erkennung von Geraden) Häufungsplateaus bilden. Ein akzeptables Ergebnis erhält man daher nur, wenn man diese Häufungsplateaus vor der Überführung in eine Geradenliste auf einen Punkt zusammenzieht. Dies kann durch einen lokalen Operator in Fenstertechnik erreicht werden.
  • Die Hough-Transformation für Geraden liefert, wie ihr Name schon aussagt, Geraden – also unendlich lange Linien ohne Start- und Endpunkt. In einem realen Kantenbild ist die Erkennung von Anfang und Endpunkt einer Kante jedoch meist von entscheidender Bedeutung, es ist also noch eine Nachverarbeitung der Geradenliste erforderlich. Ein möglicher Ansatz ist das sogenannte Tracking: Hierbei wird ein Fenster der Länge l über die erkannte Gerade geschoben und das mittlere Pixel innerhalb dieses Fensters nur dann in die Ergebnismenge aufgenommen, wenn mehr als 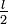\tfrac{l}{2} Pixel im Kantenbild gesetzt waren.

Weblinks

Applets zur Visualisierung der Hough-Transformation:

Literatur

  • Thomas Bräunl, Stefan Feyrer, Wolfgang Rapf, Michael Reinhardt: Parallele Bildverarbeitung. Addison-Wesley, Bonn 1995, ISBN 3-89319-951-9, S. 99ff.
  • Rafael C. Gonzales, Richard E. Woods: Digital Image Processing. Prentice Hall, New Jersey 2002, ISBN 0-201-18075-8, S. 587ff.
  • Bernd Jähne: Digitale Bildverarbeitung. 5. überarbeitete und erweiterte Auflage. Springer, Berlin 2002, ISBN 3-540-41260-3, S. 459ff.

Wikimedia Foundation.

Игры ⚽ Поможем сделать НИР

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”