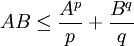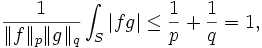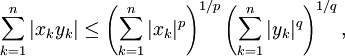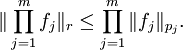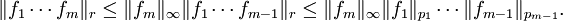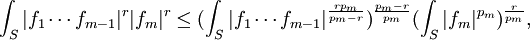- Höldersche Ungleichung
-
In der mathematischen Analysis gehört die höldersche Ungleichung, benannt nach Otto Hölder, zusammen mit der Minkowski-Ungleichung und der jensenschen Ungleichung zu den fundamentalen Ungleichungen für Lp-Räume.
Inhaltsverzeichnis
Formulierung
Sei S ein Maßraum,
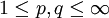 mit
mit 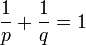 , sei f aus Lp(S) und g aus Lq(S). Dann ist fg aus L1(S) und
, sei f aus Lp(S) und g aus Lq(S). Dann ist fg aus L1(S) und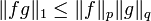 .
.
Man bezeichnet q als den zu p konjugierten Hölder-Exponenten.
Beweis
Da die Aussage für
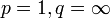 (und umgekehrt) trivial ist, sei
(und umgekehrt) trivial ist, sei 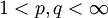 . Ohne Einschränkung seien
. Ohne Einschränkung seien 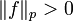 und
und 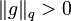 . Nach der youngschen Ungleichung gilt
. Nach der youngschen Ungleichung giltfür alle
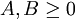 . Setze hierin speziell
. Setze hierin speziell 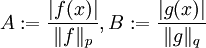 ein. Integration liefert
ein. Integration liefertwelches die höldersche Ungleichung impliziert.

Spezialfälle
Sei S die Menge
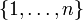 , ausgestattet mit dem Zählmaß, so erhält man als Spezialfall die Ungleichung
, ausgestattet mit dem Zählmaß, so erhält man als Spezialfall die Ungleichunggültig für alle reellen (oder komplexen) Zahlen
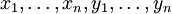 . Ist S die Menge der natürlichen Zahlen mit dem Zählmaß, erhält man eine ähnliche Ungleichung für unendliche Reihen.
. Ist S die Menge der natürlichen Zahlen mit dem Zählmaß, erhält man eine ähnliche Ungleichung für unendliche Reihen.Für p = q = 2 erhält man als Spezialfall die Cauchy-Schwarz-Ungleichung.
Verallgemeinerung
Es seien
![p_j \in [1, \infty], j = 1, \ldots, m](/pictures/dewiki/50/2f2ba76a0f84d19262564454b3c43ea7.png) sowie
sowie 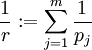 und
und 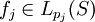 für alle
für alle 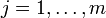 . Dann folgt
. Dann folgt 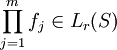 , und es gilt die Abschätzung
, und es gilt die AbschätzungBeweis
Der Beweis wird per vollständiger Induktion über m geführt. m = 1 ist trivial. Sei also nun
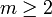 und ohne Einschränkung
und ohne Einschränkung  . Es sind zwei Fälle zu unterscheiden:
. Es sind zwei Fälle zu unterscheiden:Fall 1:
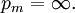 Dann ist
Dann ist 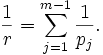 Nach Induktionsvoraussetzung gilt dann
Nach Induktionsvoraussetzung gilt dannFall 2:
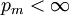 . Nach der (üblichen) hölderschen Ungleichung für die Exponenten
. Nach der (üblichen) hölderschen Ungleichung für die Exponenten 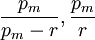 gilt
giltalso
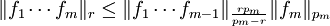 . Nun ist
. Nun ist 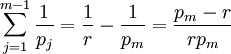 . Aus der Induktionsvoraussetzung ergibt sich somit der Induktionsschritt.
. Aus der Induktionsvoraussetzung ergibt sich somit der Induktionsschritt.
Anwendungen
- Mit der hölderschen Ungleichung kann man die Minkowski-Ungleichung (das ist die Dreiecksungleichung im Lp) leicht beweisen.
- Seien
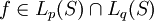 und
und 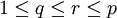 . Dann folgt
. Dann folgt 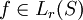 , und es gilt die Interpolationsungleichung
, und es gilt die Interpolationsungleichung
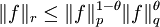 mit
mit 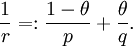
Beweis: Ohne Einschränkung sei q < r < p. Fixiere
 mit
mit  . Beachte, dass
. Beachte, dass  und
und  konjugierte Hölder-Exponenten sind. Aus der hölderschen Ungleichung folgt
konjugierte Hölder-Exponenten sind. Aus der hölderschen Ungleichung folgtPotenzieren der Ungleichung mit
 und Ausrechnen der Exponenten impliziert die Interpolationsungleichung.
und Ausrechnen der Exponenten impliziert die Interpolationsungleichung.
- Eine weitere typische Anwendung ist der Beweis der verallgemeinerten youngschen Ungleichung (für Faltungsintegrale)
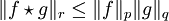 für
für 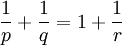 und
und 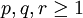 .
.
- Es gilt die folgende umgekehrte höldersche Ungleichung
 für alle r > 1,
für alle r > 1,
falls
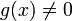 für fast alle
für fast alle 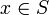 gilt und S keine Nullmenge ist.
gilt und S keine Nullmenge ist.Beweis: Wegen der (üblichen) hölderschen Ungleichung mit den Exponenten r und
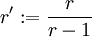 gilt
giltUmformen dieser Ungleichung liefert die umgekehrte höldersche Ungleichung.

Literatur
- Herbert Amann, Joachim Escher: Analysis III. 1. Auflage. Birkhäuser-Verlag, Basel/Boston/Berlin 2001, ISBN 3-7643-6613-3.
Wikimedia Foundation.