Inferenzregeln

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Dieser Artikel oder Abschnitt ist nicht hinreichend mit Belegen (Literatur, Webseiten oder Einzelnachweisen) versehen. Die fraglichen Angaben werden daher möglicherweise demnächst gelöscht. Hilf Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst. Bitte entferne erst danach diese Warnmarkierung.

Schlussregel bezeichnet in der formalen Logik eine Transformationsregel (Umformungsregel) in einem logischen Kalkül, d. h. eine Regel, die es erlaubt, bestehende Ausdrücke einer formalen Sprache so umzuformen, dass daraus neue Ausdrücke entstehen, die aus den bestehenden Ausdrücken folgen. Die genaue Beschaffenheit der Schlussregeln hängt davon ab, für welches logische System der Kalkül aufgestellt wird. Für die klassische, zweiwertige Logik ist Folgerung definiert als der Erhalt von Wahrheit („aus Wahrem folgt nur Wahres“). Schlussregeln sind dann so beschaffen, dass sie aus bestehenden Sätzen solche Sätze erzeugen, die schon (aber nicht notwendigerweise nur) dann wahr sind, wenn die Ausgangssätze wahr sind.

Schlussregeln sind rein syntaktisch definiert, d. h. basierend auf der Folge abstrakter Symbole, und können daher ohne Kenntnis von Inhalt (Semantik) angewandt werden. Die Anwendung einer endlichen Folge von Schlussregeln bezeichnet man als Ableitung oder auch als Beweis.

Fünf „klassische“ Schlussregeln sind Folgende:

1) Modus ponendo ponens (lat. durch Bejahung bejahende Schlussweise, Schnittregel): der direkte Beweis

$p \rightarrow q \qquad p \over q$

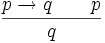
In Worten: Wenn p eine hinreichende Bedingung für q ist und p wahr ist, dann ist auch q wahr

2) Modus tollendo tollens (lat. durch Verneinung verneinende Schlussweise): der indirekte Beweis

$p \rightarrow q \qquad \neg q \over \neg p$

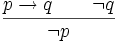
In Worten: Wenn p eine hinreichende Bedingung für q ist und q nicht wahr ist, dann ist auch p nicht wahr

3) Kettenschluss (gelegentlich – eigentlich falsch, weil nach einer anderen Bedeutung des Wortes „Kettenschluss“ – Modus Barbara genannt)

$p \rightarrow q \qquad q \rightarrow r \over p \rightarrow r$

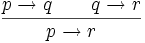
In Worten: Wenn p eine hinreichende Bedingung für q ist und q eine hinreichende Bedingung für r ist, dann ist p eine hinreichende Bedingung für r

4) Modus tollendo ponens (gelegentlich falsch Disjunktiver Syllogismus genannt)

$p \or q \qquad \neg p \over q$

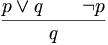
In Worten: Wenn p oder q gilt und p nicht wahr ist, dann ist q wahr

5) Widerspruch

$\neg p\rightarrow (q\land \neg q) \over p$

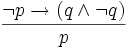
In Worten: Wenn nicht-p eine hinreichende Bedingung dafür ist, dass ein Widerspruch wahr wird, dann ist p wahr (denn ein Widerspruch kann ja nicht wahr werden)

Andere bekannte Schlussregeln sind Modus ponendo tollens, Kontraposition, Einsetzungsregel und Ersetzungsregel. Kalküle des natürlichen Schließens umfassen üblicherweise eine größere Zahl von Schlussregeln; für weitere Beispiele üblicher Schlussregeln siehe daher den Artikel Systeme natürlichen Schließens.

Keine gültige Schlussregel ist die Abduktion. Sie wird dennoch in der Künstlichen Intelligenz und Wissensrepräsentation eingesetzt, um „gesunden Menschenverstand“ zu simulieren.

Schlüsse, die letztlich nur ihre eigenen Voraussetzungen folgern, heißen Zirkelschlüsse. Obwohl rein logisch korrekt, liefern sie keine neue Erkenntnis, weil jede Aussage trivialerweise aus sich selbst folgt.

Logische Aussagen lassen sich auch durch Resolutionsregeln umformulieren. Auf diese Weise lassen sich bestimmte Typen von Schlussfolgerungen als Widerspruchsbeweise automatisieren.

Siehe auch: Aussagenkalkül, Ableitung (Logik), Schlussfolgerung, gültige Regel; Dilemma