- Lambdakalkül
-
Der Lambda-Kalkül ist eine formale Sprache zur Untersuchung von Funktionen, die Funktionsdefinitionen, das Definieren formaler, sowie das Auswerten und Einsetzen aktueller Parameter regelt.
Inhaltsverzeichnis
Geschichte
Der Lambda-Kalkül wurde von Alonzo Church und Stephen Kleene in den 1930er Jahren eingeführt. Church benutzte ihn, sowohl um 1936 eine negative Antwort auf das Entscheidungsproblem zu geben, als auch eine Fundierung eines logischen Systems zu finden, wie es Russells und Whiteheads Principia Mathematica zugrunde lag. Mittels des untypisierten Lambda-Kalküls kann man klar definieren, was eine berechenbare Funktion ist. Die Frage, ob zwei Lambda-Ausdrücke (s.u.) äquivalent sind, kann im Allgemeinen nicht algorithmisch entschieden werden. In seiner typisierten Form kann der Kalkül benutzt werden, um Logik höherer Stufe darzustellen. Der Lambda-Kalkül hat die Entwicklung funktionaler Programmiersprachen, die Forschung um Typsysteme von Programmiersprachen im Allgemeinen als auch moderne Teildisziplinen in der Logik wie Typtheorie wesentlich beeinflusst.
Meilensteine der Entwicklung waren im Einzelnen:
- Nach der Einführung die frühe Entdeckung, dass sich mit dem Lambda-Kalkül alles ausdrücken lässt, was man mit einer modernen Programmiersprache oder der Turing-Maschine ausdrücken kann. In anderen Worten: Im Sinne des Konzepts der Berechenbarkeit sind die drei gleich mächtig.
- Konrad Zuse hat Ideen aus dem Lambda-Kalkül 1942 bis 1946 in seinen Plankalkül einfließen lassen.
- John McCarthy hat sie Ende der fünfziger Jahre verwendet und damit die minimalen Funktionen der Programmiersprache LISP definiert.
- Die typisierten Varianten des Lambda-Kalküls führten zu modernen Programmiersprachen wie ML oder Haskell.
- Als überaus fruchtbar erwies sich die Idee, Ausdrücke des typisierten Lambda-Kalküls zur Repräsentation von Termen einer Logik zugrunde zu legen, den Lambda-Kalkül also als Meta-Logik zu verwenden. Erstmals von Church 1940 in seiner Theory of Simple Types präsentiert, führte sie einerseits zu modernen Theorembeweisern für Logiken höherer Stufe und …
- andererseits in den 70er und 80er Jahren zu Logiken mit immer mächtigeren Typsystemen, in dem sich z. B. logische Beweise an sich als Lambda-Ausdruck darstellen lassen.
- In Anlehnung an den Lambda-Kalkül wurde für die Beschreibung nebenläufiger Prozesse der Pi-Kalkül von Robin Milner in den 90er Jahren entwickelt.
Der untypisierte Lambda-Kalkül
Einführung
Im Lambda-Kalkül geht es im Wesentlichen um Ausdrücke und ihre Umformung. Um den Lambda-Kalkül auf ein Problem anzuwenden, konstruiert man Ausdrücke, die sich wie das Problem verhalten – so wie man beim Lösen von Textaufgaben in der Mathematik auch vorgehen kann. Der Lambda-Kalkül kann auf vielfältigere Probleme angewandt werden als beispielsweise die auch bei Nicht-Mathematikern weit verbreiteten Rechenmethoden.
Im Lambda-Kalkül steht jeder Ausdruck für eine Funktion mit nur einem Argument; sowohl Argumente als auch Resultate solcher Funktionen sind wiederum Funktionen. Eine Funktion kann anonym durch eine so genannte Lambda-Abstraktion definiert werden, die die Zuordnung des Arguments zum Resultat beschreibt. Zum Beispiel wird die erhöhe-um-2 Funktion f(x) = x + 2 im Lambda-Kalkül durch die Lambda-Abstraktion λ x. x + 2 (oder äquivalent durch λ y. y + 2; der Name des formalen Parameters ist unerheblich) beschrieben; f(3) (die so genannte Funktionsanwendung) kann daher als (λ x. x + 2) 3 geschrieben werden. Die Funktionsanwendung ist linksassoziativ: f x y ist syntaktisch gleichbedeutend mit (f x) y. Offensichtlich sollten die Ausdrücke: (λ x. x +3) ((λ x. x+2) 0 ) und (λ x. x + 3) 2 und 2 + 3 äquivalent sein – dies motiviert die β-Kongruenzregel (siehe unten). Eine zweistellige Funktion kann im Lambda-Kalkül durch eine einstellige Funktion dargestellt werden, die eine einstellige Funktion als Resultat zurückgibt (siehe auch Schönfinkeln bzw. Currying). Die Funktion f(x, y) = x − y kann zum Beispiel durch λ x. λ y. x − y dargestellt werden. Denn mit der β-Kongruenzregel sind die Ausdrücke (λ x. λ y. x − y) 7 2, (λ y. 7 − y) 2 und 7−2 äquivalent.
Nicht jeder Lambda-Ausdruck kann auf definite Werte reduziert werden wie im obigen Beispiel. Man betrachte z. B.
- (λ x. x x) (λ x. x x)
oder
- (λ x. x x x) (λ x. x x x)
und ermittele die β-kongruenten Terme, um sich ein Bild zu machen. (λ x. x x) wird auch als Ω-Kombinator bezeichnet; ((λ x. x x) (λ x. x x)) heißt Ω. Dementsprechend ist ((λ x. x x x) (λ x. x x x)) Ω2 etc.
Streng genommen enthält der Lambda-Kalkül keine Symbole für die Zahlen und die Addition. Allerdings zeigt sich, dass sie als Abkürzungen für Lambda-Ausdrücke innerhalb des Kalküls beschrieben werden können (siehe unten).
Die Ausdrücke des Lambda-Kalküls können freie Variablen enthalten, d. h. Variablen, die nicht durch ein außenstehendes λ gebunden sind. Zum Beispiel ist die Variable y in dem Ausdruck (λ x. y) frei; sie repräsentiert eine Funktion, die stets das Resultat y ergibt. Dies macht im Allgemeinen die Umbenennung von formalen Parametern notwendig, z. B. wenn
- (λ x. λ y. y x) (λ x. y)
auf
- λ z. z (λ x. y)
abgeleitet werden soll.
Ein Spezialfall des Lambda-Kalküls ist die sogenannte Kombinatorische Logik.
Formale Definition
In seiner einfachsten, dennoch vollständigen Form gibt es im Lambda-Kalkül drei Sorten von Termen (T), hier in Backus-Naur-Form:
T ::= a (Variable) | (T T) (Applikation) | λa.T (Lambda, auch Abstraktion genannt)
wobei a für ein beliebiges Symbol aus einer mindestens abzählbar-unendlichen Menge von Variablensymbolen (kurz: Variablen) steht. Für praktische Zwecke wird der Lambda-Kalkül üblicherweise noch um eine weitere Sorte von Termen, den Konstantensymbolen, erweitert.
Die Menge der freien Variablen FV kann induktiv über der Struktur der λ-Terme wie folgt definiert werden:
- FV(a) = {a}, falls der Term eine Variable a
- FV(T1 T2) = FV(T1) ∪ FV(T2) für Applikationen, und
- FV(λ a. T) = FV(T)\{a}, falls der Term eine Abstraktion ist, sind seine freien Variablen die freien Variablen von T außer a.
Die Menge der gebundenen Variablen B(T) eines Terms T errechnet sich auch induktiv:
- B(a) = {}, falls der Term eine Variable a
- B(T1 T2) = B(T1) ∪ B(T2) für Applikationen, und
- B(λ a. T) = B(T)∪{a}, falls der Term eine Abstraktion ist, sind seine gebundenen Variablen die gebundenen Variablen von T vereinigt a.
Mittels der Definition von freien und gebundenen Variablen kann nun der Begriff der (freien) Variablensubstitution (Einsetzung) induktiv definiert werden durch:
- a[x ← T] = a falls Variable x ungleich a
- a[a ← T] = T
- (T1 T2)[x ← T] = (T1[x ← T] T2[x ← T])
- (λ a. T')[a ← T] = (λ a. T')
- (λ a. T')[x ← T] = (λ a. T'[x ← T]) falls Variable x ungleich a und falls FV(T) disjunkt von B(λ a. T').
Hinweis: x ← T stehe für die Ersetzung von x durch T.
Man beachte, dass die Substitution nur partiell definiert ist; ggf. müssen gebundene Variablen geeignet umbenannt werden (siehe α-Kongruenz im Folgenden), so dass niemals eine freie Variable in einem Substitut durch Einsetzung für eine Variable gebunden wird.
Über der Menge der λ-Terme können nun Kongruenzregeln (hier == geschrieben) definiert werden, die die Intuition formal fassen, dass zwei Ausdrücke dieselbe Funktion beschreiben. Diese Relationen sind durch die sogenannte α-Konversion, die β-Konversion sowie die η-Konversion erfasst.
Kongruenzregeln
α-Konversion
Die α-Konversionsregel formalisiert die Idee, dass die Namen von gebundenen Variablen „Schall und Rauch“ sind; z. B. bedeuten λx.x und λy.y dieselbe Funktion. Allerdings sind die Details nicht ganz so einfach wie es zunächst erscheint: Eine Reihe von Einschränkungen müssen beachtet werden, wenn gebundene Variablen durch andere gebundene Variablen ersetzt werden.
Formal lautet die Regel wie folgt:
- λ V. E == λ W. E[V←W]
falls W in E nirgends frei vorkommt und W in E dort nicht gebunden ist, wo es ein V ersetzt. Da eine Kongruenzregel in jedem Teilterm anwendbar ist, erlaubt sie die Ableitung, dass λ x. (λ x. x) x gleich λ y. (λ x. x) y ist.
β-Konversion
Die β-Konversionsregel formalisiert das Konzept der „Funktionsanwendung“. Wird sie ausschließlich von links nach rechts angewandt, spricht man auch von β-Reduktion. Formal lässt sie sich durch
- ((λ V. E ) E' ) == E [V←E' ]
beschreiben, wobei alle freien Variablen in E' in E [V←E' ] frei bleiben müssen (siehe Nebenbedingung bei der Substitutionsdefinition).
Ein Term heißt „in β-Normalform“, wenn keine β-Reduktion mehr anwendbar ist (nicht für alle Terme existiert eine β-Normalform; siehe Ω). Ein tiefes Resultat von Church und Rosser über den λ-Kalkül besagt, dass die Reihenfolgen von α-Konversionen und β-Reduktionen in gewissem Sinn keine Rolle spielt: wenn man einen Term zu zwei Termen T1 und T2 ableitet, gibt es immer eine Möglichkeit, T1 und T2 jeweils zu einem gemeinsamen Term T3 abzuleiten.
η-Konversion
Die η-Konversion kann optional zum Kalkül hinzugefügt werden. Sie formalisiert das Konzept der Extensionalität, d. h. dass zwei Funktionen genau dann gleich sind, wenn sie für alle Argumente dasselbe Resultat liefern. Formal ist die η-Konversion beschrieben durch:
- λ x . f x == f, wenn x nicht freie Variable von f ist.
Anmerkungen
- Jeder Term, der die Bedingung der β-Regel erfüllt, wird β-reduzibel genannt.
- Die β-Reduktion ist im Allgemeinen nicht eindeutig; es kann mehrere „Ansatzpunkte“ (β-Redexe) für die Anwendung der β-Regel geben, weil die Regelanwendung in allen Teiltermen möglich ist.
- Wenn mehrere Folgen von β-Reduktionen möglich sind und mehrere davon zu einem nicht-β-reduziblen Term führen, so sind diese Terme bis auf α-Kongruenz gleich.
- Wenn jedoch eine Reihenfolge der β zu einem nicht-β-reduziblen Term (einem Ergebnis) führt, so tut dies auch die Standard Reduction Order, bei der das im Term erste Lambda zuerst verwendet wird.
- Bei der so genannten de-Bruijn-Notation werden die Variablennamen weggelassen. Stattdessen werden Zahlen geschrieben, die die Anzahl der Lambda-Terme zwischen der Variable (also eine Zahl) und dem bindenden Lambda-Ausdruck angibt. Diese Darstellung wird oft in Computerprogrammen verwendet.
Weitere Beispiele
- Wenn man wahr als Abkürzung für λx.λy.x versteht und falsch als Abkürzung für λx.λy.y, dann ist der Term λx.λy.((x y) falsch) eine Möglichkeit (von vielen), die logische Funktion und darzustellen, denn er erfüllt die Forderungen, die man an die Funktion und stellt:
- ((und wahr) wahr) = (((λx.λy.((x y) falsch)) wahr) wahr) = (wahr wahr) falsch = ((λx.λy.x) wahr) falsch = (λy.wahr) falsch = wahr
- ((und wahr) falsch) = … = (wahr falsch) falsch = … = (λy.falsch) falsch = falsch
- ((und falsch) wahr) = (falsch wahr) falsch = ((λx.λy.y) wahr) falsch = (λy.y) falsch = falsch
- ((und falsch) falsch) = (falsch falsch) falsch = … = (λy.y) falsch = falsch
- Man kann in ähnlicher Weise Zahlen, Tupel und Listen in λ-Ausdrücken codieren (z. B. durch sogenannte Church-Numerale)
- Man kann beliebige rekursive Funktionen durch den Fixpunkt-Kombinator Y (= λ g. (λ x. g (x x)) (λ x. g (x x))) darstellen.
Typisierter Lambda-Kalkül
Die zentrale Idee typisierten Lambda-Kalküls ist es, nur noch Lambda-Ausdrücke zu betrachten, denen sich ein Typ durch ein System von Typinferenzregeln zuordnen lässt. Das einfachste Typsystem, das von Church 1940 in seiner Theory of Simple Types vorgestellt wurde, sieht die Typen vor, die durch folgende Grammatik in Backus-Naur-Form generiert werden:
Den Typ I (individuals) kann man sich als Zahlen vorstellen, O wird für boolesche Werte wie True und False verwendet.
Zusätzlich wird eine Umgebung Γ definiert; dies ist eine Funktion, die Variablensymbolen Typen TT zuordnet.
Ein Tripel aus einer Umgebung Γ, einem Ausdruck E und einem Typ T, geschrieben
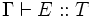 wird ein Typurteil genannt.
wird ein Typurteil genannt.Nun können die Inferenzregeln Beziehungen zwischen Ausdrücken, ihren Typen und Typurteilen herstellen:
Hierbei ist
![{\Gamma[a \mapsto\tau]}](/pictures/dewiki/101/ef9c4dfe1c508714678d4b8897ab2028.png) diejenige Funktion, die an der Stelle a den Typ τ zuordnet, und ansonsten die Funktion Γ ist.
diejenige Funktion, die an der Stelle a den Typ τ zuordnet, und ansonsten die Funktion Γ ist.Durch Einführung einer zweiten Umgebung sind auch Konstantensymbole behandelbar; eine weitere wichtige Erweiterung besteht darin, in Typen auch die Kategorie der Typvariablen α,β,γ,etc oder Typkonstruktoren wie Set(α),List(β),etc zuzulassen: so entstehen schon sehr mächtige funktionale oder logische Kernsprachen.
Es ist entscheidbar, ob ein untypisierter Term sich typisieren lässt, selbst wenn die Umgebung Γ unbekannt ist (eine Variante mit Typvariablen und Typkonstruktoren ist Milners Algorithm W).
Die Menge der typisierbaren Ausdrücke ist eine echte Teilmenge des untypisierten Lambda-Kalküls; z. B. lässt sich der Y-Kombinator nicht typisieren. Andererseits ist für typisierte Ausdrücke die Gleichheit zwischen zwei Funktionen modulo α und β Konversionen entscheidbar. Es ist bekannt, dass das Matching-Problem auf Lambda-Ausdrücken bis zur vierten Ordnung entscheidbar ist. Das Unifikationsproblem ist unentscheidbar; allerdings gibt es praktisch brauchbare approximative Algorithmen.
Anwendung in der Semantik
Die Semantik ist dasjenige Teilgebiet der Linguistik, welches die Bedeutung natürlichsprachlicher Ausdrücke analysiert. Die formale Semantik nutzt dazu zunächst einfache Mittel der Prädikatenlogik und Mengenlehre. Diese erweitert man um Grundlagen des Lambda-Kalküls, etwa um mittels Lambda-Abstraktion Propositionen als Eigenschaften zu repräsentieren und komplexere Nominalphrasen, Adjektivphrasen und einige Verbalphrasen darstellen zu können. Grundlage ist etwa eine modelltheoretische semantische Interpretation der intensionalen Logik Richard Montagues.
Siehe auch
Weblinks
- Das gefürchtete Lambda-Kalkül Eine Einführung.
- Einführung in den λ-Kalkül Gute, etwas flippige Einführung in den λ-Kalkül (ca. 100 Seiten, als PS- und PDF-Dokument)
- Stephen Kleene, A theory of positive integers in formal logic, American Journal of Mathematics, 57 (1935), pp 153–173 and 219–244. Enthält eine Sammlung von Funktionen im λ-Kalkül.
- Alonzo Church, An unsolvable problem of elementary number theory, American Journal of Mathematics, 58 (1936), pp 345–363. Dieses Papier enthält den Beweis, dass die Äquivalenz von Ausdrücken unentscheidbar ist.
- Jim Larson, An Introduction to Lambda Calculus and Scheme. Eine einfache Einführung für Programmierer.
Literatur
- Henk Barendregt: The lambda calculus, its syntax and semantics. North-Holland, 1984, ISBN 978-0-444-87508-2
- Roberto M. Amadio, Pierre-Louis Curien: Domains and Lambda Calculi. Cambridge University Press, 1998, ISBN 0521622778
- Guo-Qiang Zhang: Logic of Domains. Springer, 1991, ISBN 978-0-8176-3570-1
- Samson Abramsky: Typed Lambda Calculi and Applications. Springer, 2001, ISBN 978-3-540-41960-0
Wikimedia Foundation.

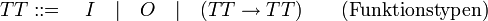
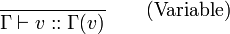
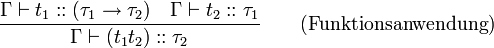
![{ \Gamma[a \mapsto\tau_1] \vdash t :: \tau_2 \over \Gamma \vdash \lambda a. t :: \tau_1 \rarr \tau_2}\qquad ({\rm Abstraktion})](/pictures/dewiki/97/a50e6a32749c757d9df1a1773017e6f3.png)