- Infinitesimaler Operator
-
Der infinitesimale Generator eines zeithomogenen Markow-Prozess in stetiger Zeit mit nicht unbedingt abzählbarem Zustandsraum ist ein Operator, welcher das stochastische Verhalten des Prozesses in infinitesimaler Zeit erfasst. Er ist in gewisser Hinsicht eine Form der Ableitung der Übergangswahrscheinlichkeiten Pt(x,A) nach der Zeit und eine Verallgemeinerung der Q-Matrix eines zeithomogenen Markow-Prozesses in stetiger Zeit mit abzählbarem Zustandsraum. Aufgrund der Markow-Eigenschaft und der zeitlichen Homogenität wird der Prozess unter bestimmten Voraussetzungen durch seinen infinitesimalen Generator bestimmt oder, in anderer Sprechweise, generiert.
Inhaltsverzeichnis
Definition nach Breiman
Gegeben ein zeithomogener Markow-Prozess
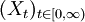 auf dem Zustandsraum
auf dem Zustandsraum 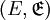 , dann ist der Generator A von (Xt) für beschränktes, borelmessbares
, dann ist der Generator A von (Xt) für beschränktes, borelmessbares 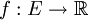 punktweise definiert über
punktweise definiert übersofern der Grenzwert für alle
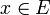 existiert. Die Menge der Funktionen, für die der Grenzwert existiert, ist der Definitionsbereich von A und wird mit
existiert. Die Menge der Funktionen, für die der Grenzwert existiert, ist der Definitionsbereich von A und wird mit 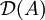 bezeichnet.
bezeichnet.Generatoren von Feller-Prozessen
Feller-Prozesse sind Markow-Prozesse, bei denen die Übergangswahrscheinlichkeiten Pt(x,A) qua
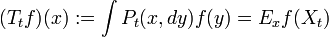 einer stark stetigen Halbgruppe auf dem Raum C0(E) der stetigen, im Unendlichen verschwindenden Funktionen entsprechen. In diesem Fall kann der Generator der entsprechenden Halbgruppe
einer stark stetigen Halbgruppe auf dem Raum C0(E) der stetigen, im Unendlichen verschwindenden Funktionen entsprechen. In diesem Fall kann der Generator der entsprechenden Halbgruppe(definiert für alle
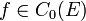 für die der Grenzwert bezüglich der Supremumsnorm existiert) betrachtet und der Satz von Hille-Yosida angewendet werden.
für die der Grenzwert bezüglich der Supremumsnorm existiert) betrachtet und der Satz von Hille-Yosida angewendet werden.Dynkins charakteristischer Operator
Der charakteristische Operator ist eine probabilistische Entsprechung des analytischen Generators S, mit dem oft leichter zu arbeiten ist.[1] Während in obiger Definition der Erwartungswert von f(Xt) zu einem festen Zeitpunkt t gebildet wird (und anschließend t gegen 0 geht), wird hier der Erwartungswert von f(Xτ) an den unterschiedlichen (zufälligen) Zeitpunkten τ = τ(B) gebildet, zu denen der Prozess einen festgelegten räumlichen Bereich B, zum Beispiel eine Kugel Bν,x um x = X0 mit Radius ν, verlässt. Für nicht absorbierendes x setzt man
für absorbierendes x man (Uf)(x) = 0. Für große Klasse von Feller-Prozessen gilt Af = Uf für stetige, im Unendlichen verschwindende Funktionen f aufgrund von Dynkins Maximum-Prinzip.
Die Definition und der genannte Zusammenhang gehen auf eine Arbeit von E. B. Dynkin aus dem Jahr 1955 zurück. [2]
Literatur
- Leo Breiman: Probability. Addison-Wesley Publishing Company, Reading, Massachusetts, 1968.
- Bernt Øksendal: Stochastic Differential Equations. An Introduction with Applications, Springer Berlin 2003, ISBN 3-540-04758-1
- Daniel Revuz, Marc Yor: Continuous Martingales and Brownian Motion, Springer 2001, ISBN 3-540-64325-7
Einzelnachweise
Wikimedia Foundation.

![A f(x)=\lim_{t\to0}\frac{E_x[f(X_t)]-f(x)}{t},\ x\in E,](/pictures/dewiki/101/e6280fabc5bbfc8bdc35a85255d19b99.png)
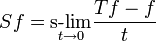
![(U f) (x) := \lim_{\nu\to0} \frac{E_x [f(X_{\tau(B_{\nu,x})})] - f(x)}{E_x[\tau(B_{\nu,x})]},](/pictures/dewiki/99/c86fea8ac0361ac8fad5cfd5ad5f0351.png)