- Propagationsoperator
-
Der Zeitentwicklungsoperator ist ein quantenmechanischer Operator, mit dem sich die zeitliche Entwicklung eines physikalischen Systems berechnen lässt. Der quantenmechanische Operator ist eng verwandt mit dem Propagator in der Quantenfeld- oder Vielteilchentheorie. Üblicherweise wird er als U(t,t0) geschrieben und hat folgende Eigenschaften:
Definierende Eigenschaften:
- Haupteigenschaft:
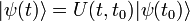
damit folgt physikalisch:
- Kontinuität: U(t0,t0) = 1
- Schrödinger-Gleichung:
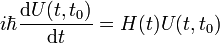
daraus folgende Eigenschaften:
- Unitarität zum Erhalt der Gesamtwahrscheinlichkeit
- Komposition: U(t2,t0) = U(t2,t1)U(t1,t0)
Der infinitesimale Zeitentwicklungs-Operator hat die Form:
Ein nichtinfinitesimaler Zeitentwicklungs-Operator kann, je nachdem ob der Hamiltonoperator zeitabhängig ist und mit sich selbst zu unterschiedlichen Zeiten kommutiert, unterschiedliche Formen annehmen. Im einfachsten Fall ist H unabhängig von der Zeit und es gilt
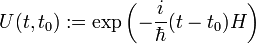 .
.
Ist H = H(t) zeitabhängig, verallgemeinert man
mit dem Zeitordnungs-Operator T.
Inhaltsverzeichnis
Herleitung des Zeitentwicklungsoperators
Durch Anwenden des Zeitentwicklungsoperators U(t) auf einen Zustandsvektor zum Zeitpunkt t0 = 0 erhält man den Zustandsvektor zum Zeitpunkt t. Im Folgenden wird stets die abkürzende Schreibweise U(t,0) = U(t) verwendet:
Einsetzen der zeitabhängigen Wellenfunktion in die Schrödingergleichung:
Man bekommt eine zur Schrödingergleichung äquivalente Operatorgleichung, formal eine gewöhnliche Differentialgleichung 1. Ordnung
Zeitunabhängiger Hamiltonoperator
Für einen zeitunabhängigen Hamiltonoperator
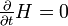 wird die Operatorgleichung
wird die Operatorgleichungdurch
gelöst.
Infinitesimaler Zeitentwicklungsoperator
Entwickelt man das gerade erhaltene Ergebnis bis zur ersten Ordnung in der Zeit
erhält man für
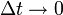 den infinitesimalen Zeitentwicklungsoperator, wobei ab hier der Hamiltonoperator auch explizit zeitabhängig sein kann:
den infinitesimalen Zeitentwicklungsoperator, wobei ab hier der Hamiltonoperator auch explizit zeitabhängig sein kann:Das Produkt mit seinem adjungierten Operator
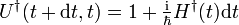 ergibt 1, weil der Hamiltonoperator hermitesch ist
ergibt 1, weil der Hamiltonoperator hermitesch ist 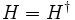 . Also ist U(t + dt,t) unitär:
. Also ist U(t + dt,t) unitär:Der vollständige Zeitentwicklungsoperator U(t,0) lässt sich als Produkt infinitesimaler Zeitentwicklungsoperatoren schreiben:
Das Produkt unitärer Operatoren ist ebenfalls unitär, also auch der vollständige Zeitentwicklungsoperator.
Die Aussagen zur Unitarität lassen sich auch in entgegengesetzter Richtung nachvollziehen: Die Wahrscheinlichkeitsinterpretation der Quantenmechanik fordert, dass die Norm eines Zustands
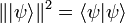 zeitlich erhalten bleibt. Deshalb muss der Zeitentwicklungsoperator unitär bzw. der Hamiltonoperator hermitesch sein. Mit
zeitlich erhalten bleibt. Deshalb muss der Zeitentwicklungsoperator unitär bzw. der Hamiltonoperator hermitesch sein. Mit 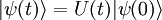 und
und 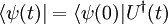 folgt:
folgt:Zeitabhängiger Hamiltonoperator
Für einen zeitabhängigen Hamiltonoperator schreibt man die Differentialgleichung
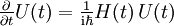 durch Zeitintegration
durch Zeitintegrationin eine Integralgleichung um:
Diese setzt man rekursiv in sich ein:
Man erhält für den Zeitentwicklungsoperator eine Reihe (Neumann-Reihe)
dabei ist der n-te Summand:
Im Integranden stehen die früheren Zeiten weiter rechts als die späteren, z.B. gilt stets
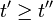 , da t' die obere Integrationsgrenze bei der t'' Integration ist. Im Allgemeinen vertauschen die Hamiltonoperatoren zu verschiedenen Zeiten nicht miteinander. Dies ist der Grund wieso das Ergebnis des zeitunabhängigen Hamiltonoperators nicht einfach übertragbar ist.
, da t' die obere Integrationsgrenze bei der t'' Integration ist. Im Allgemeinen vertauschen die Hamiltonoperatoren zu verschiedenen Zeiten nicht miteinander. Dies ist der Grund wieso das Ergebnis des zeitunabhängigen Hamiltonoperators nicht einfach übertragbar ist.![\left[H(t_{1}),H(t_{2})\right]\neq 0](/pictures/dewiki/48/0099ba3a9dcff901be957b2ba5ea4517.png) für
für 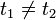
Durch Verwendung von Heaviside-Funktionen Θ(t) lassen sich alle Integrationen von 0 bis t ausführen. Dadurch kann nun die Reihenfolge der Integrationen vertauscht werden.
Dieser Ausdruck ist invariant bei Vertauschung zweier beliebiger Zeitargumente t(i) und t(j). Da die Stufenfunktionen für die Zeitordnung im Integranden sorgen, definiert man daran angelehnt den Zeitordnungsoperator T. Dieser sortiert spätere Zeiten nach links. Für zwei Operatoren:
Zeitordnungsoperator angewandt auf n Operatoren, dabei ist σ eine Permutation der Menge
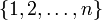 :
:Dies ergibt für Un(t), wobei ein Faktor 1 / n! hinzukommt, da es n! Möglichkeiten gibt die n Zeitargumente im Integranden anzuordnen:
Den gesamten Zeitentwicklungsoperator erhält man durch Aufsummieren:
Für zeitunabhängige H erhält man wieder obige einfache Lösung
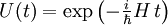 .
.Literatur
- J. J. Sakurai: Modern Quantum Mechanics. Prentice Hall, 1993. ISBN 978-0201539295
- Haupteigenschaft:
Wikimedia Foundation.

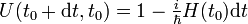
![U(t,t_0):=T\left[\exp\left(-\frac{i}{\hbar}\int_{t_0}^t H(t^\prime)dt^\prime\right)\right].](/pictures/dewiki/97/ae972e51c2a09c49700c8ff2d578d99b.png)
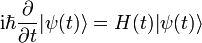
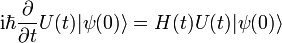
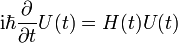
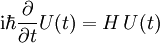
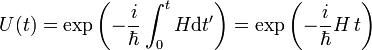
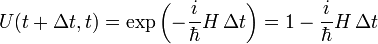
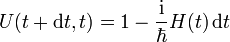
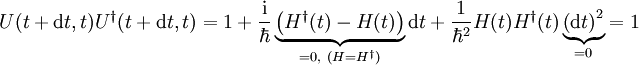
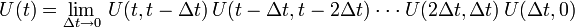
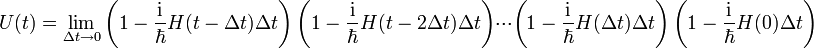
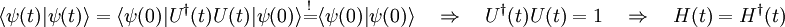
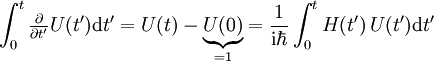
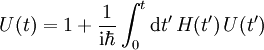
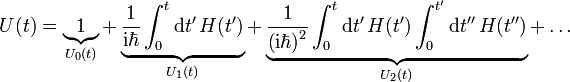
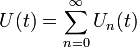
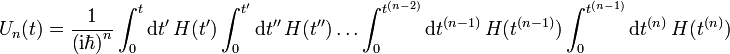
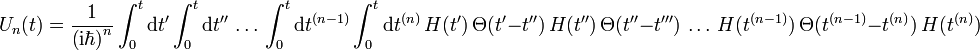
![T\left[A(t_{1}),B(t_{2})\right]=\Theta(t_{1}-t_{2})A(t_{1})B(t_{2})+\Theta(t_{2}-t_{1})B(t_{2})A(t_{1})=\begin{cases}
A(t_{1})B(t_{2}) & \ ,\ t_{1}\geq t_{2}\\
B(t_{2})A(t_{1}) & \ ,\ t_{2}>t_{1}\end{cases}](/pictures/dewiki/53/5c642b90c42a6b8da956c50c45a89a3e.png)
![T\left[H(t'),H(t''),\ldots,H(t^{(n)})\right]=H(t^{\sigma(1)})H(t^{\sigma(2)})\ldots H(t^{\sigma(n)})\ ,\quad\text{mit}\quad t^{\sigma(1)}\geq t^{\sigma(2)}\geq\ldots\geq t^{\sigma(n)}](/pictures/dewiki/98/b519455b1d942bafaefdb5e3ef172a36.png)
![U_{n}(t)=\frac{1}{n!}\frac{1}{\left(\mathrm{i}\hbar\right)^{n}}T\left[\int_{0}^{t}\mathrm{d}t'\, H(t')\int_{0}^{t}\mathrm{d}t''\, H(t'')\ldots\int_{0}^{t}\mathrm{d}t^{(n-1)}\, H(t^{(n-1)})\int_{0}^{t}\mathrm{d}t^{(n)}\, H(t^{(n)})\right]=\frac{1}{n!}\frac{1}{\left(\mathrm{i}\hbar\right)^{n}}T\left[\left(\int_{0}^{t}\mathrm{d}t'\, H(t')\right)^{n}\right]](/pictures/dewiki/57/93403eb25847b720b73880f0b9d882bd.png)
![U(t)=\sum_{n=0}^{\infty}U_{n}(t)=\sum_{n=0}^{\infty}\frac{1}{n!}\frac{1}{\left(\mathrm{i}\hbar\right)^{n}}T\left[\left(\int_{0}^{t}\mathrm{d}t'\, H(t')\right)^{n}\right]=T\left[\sum_{n=0}^{\infty}\frac{1}{n!}\frac{1}{\left(\mathrm{i}\hbar\right)^{n}}\left(\int_{0}^{t}\mathrm{d}t'\, H(t')\right)^{n}\right]=T\left[\exp\left(\frac{1}{\mathrm{i}\hbar}\int_{0}^{t}\mathrm{d}t'\, H(t')\right)\right]](/pictures/dewiki/101/e6062225f7612a12ca5fe525a4a247bc.png)
![U(t)=T\left[\exp\left(-\frac{\mathrm{i}}{\hbar}\int_{0}^{t}\mathrm{d}t'\, H(t')\right)\right]](/pictures/dewiki/51/3c89d4fede1014a58cb505bd6936300e.png)