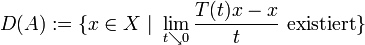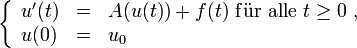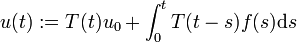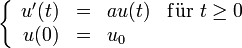- Satz von Hille-Yosida
-
Eine stark stetige Halbgruppe (gelegentlich auch als C0-Halbgruppe bezeichnet) ist eine Familie
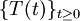 von stetigen linearen Abbildungen
von stetigen linearen Abbildungen 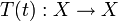 eines reellen oder komplexen Banachraums X in sich, welche die drei Eigenschaften
eines reellen oder komplexen Banachraums X in sich, welche die drei Eigenschaften- T(0) = I,
- T(s + t) = T(s)T(t) für alle
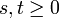 sowie
sowie 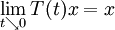 für alle
für alle 
erfüllt. Stark stetige Halbgruppen spielen eine große Rolle in der (abstrakten) Theorie der Evolutionsgleichungen.
Inhaltsverzeichnis
Klassifikation stark stetiger Halbgruppen
Zu jeder stark stetigen Halbgruppe existieren ein
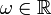 und ein
und ein 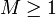 , so dass für alle
, so dass für alle 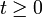 die Abschätzung
die Abschätzunggilt. Hierbei bezeichnet
 die Operatornorm auf dem Banachraum der stetigen linearen Endomorphismen von X. Man bezeichnet die Halbgruppe
die Operatornorm auf dem Banachraum der stetigen linearen Endomorphismen von X. Man bezeichnet die Halbgruppe- als Kontraktionshalbgruppe, falls dies für M = 1 und ω = 0 erfüllt ist,
- als beschränkte Halbgruppe, falls obige Ungleichung für ein
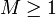 und ω = 0 gilt,
und ω = 0 gilt, - als quasi-kontraktive Halbgruppe, falls obige Ungleichung für M = 1 und ein
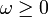 erfüllt ist.
erfüllt ist.
Das Infimum ω0 über alle möglichen ω, also
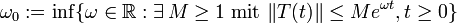 , heißt Wachstumsschranke.
, heißt Wachstumsschranke.Betrachtet man
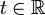 statt t > 0, spricht man von stark stetigen Gruppen.
statt t > 0, spricht man von stark stetigen Gruppen.Stark stetige Halbgruppen lassen sich unter gewissen Umständen von
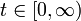 auf Sektoren in der komplexen Ebene fortsetzen. Solche Halbgruppen werden analytisch genannt.
auf Sektoren in der komplexen Ebene fortsetzen. Solche Halbgruppen werden analytisch genannt.Infinitesimaler Erzeuger
Setzt man
sowie
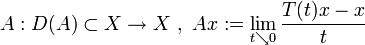 ,
,
so ist A ein dicht definierter, abgeschlossener, linearer Operator. Man nennt A den infinitesimalen Erzeuger oder Generator der Halbgruppe
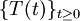 . Es gilt, dass das abstrakte Cauchy-Problem
. Es gilt, dass das abstrakte Cauchy-Problemfür den Anfangswert
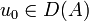 und eine stetig differenzierbare Funktion
und eine stetig differenzierbare Funktion 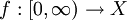 durch die Funktion
durch die Funktiongelöst wird.
Für das Spektrum des Erzeugers gilt: Ist
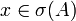 , dann gilt
, dann gilt 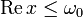 , wobei ω0 die Wachstumsschranke der Halbgruppe ist. Die Resolvente von A stimmt mit der Laplace-Transformation der Halbgruppe überein, also
, wobei ω0 die Wachstumsschranke der Halbgruppe ist. Die Resolvente von A stimmt mit der Laplace-Transformation der Halbgruppe überein, also 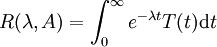 für
für 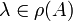 .
.Satz von Hille-Yosida
Von besonderem Interesse ist, ob ein gegebener Operator A der infinitesimale Erzeuger von einer stark stetigen Halbgruppe ist. Diese Frage wird durch den Satz von Hille-Yosida vollständig beantwortet:
Ein linearer Operator
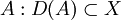 ist genau dann der infinitesimale Erzeuger einer stark stetigen Halbgruppe
ist genau dann der infinitesimale Erzeuger einer stark stetigen Halbgruppe 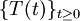 , welche die Abschätzung
, welche die Abschätzung 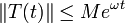 erfüllt, falls A abgeschlossen und dicht definiert ist sowie alle
erfüllt, falls A abgeschlossen und dicht definiert ist sowie alle 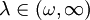 in der Resolventenmenge von A liegen mit
in der Resolventenmenge von A liegen mit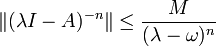 für alle λ > ω und
für alle λ > ω und  .
.
Im Anwendungsfall ist A ein gegebener Differentialoperator, und man möchte die Evolutionsgleichung u' = Au + f lösen. Der Satz von Hille-Yosida besagt, dass man hierfür die Resolventengleichung untersuchen muss, die dann auf elliptische Probleme führt. In dieser Hinsicht muss man erst das elliptische Problem verstehen, um das Evolutionsproblem zu lösen.
Herleitung
Die Theorie der stark stetigen Halbgruppen entwickelte sich aus der Betrachtung des Cauchy-Problems. Die einfachste Form des Cauchy-Problems ist die Fragestellung, ob für ein gegebenes
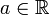 und ein Anfangswert
und ein Anfangswert 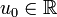 eine differenzierbare Funktion
eine differenzierbare Funktion 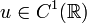 existiert, die
existiert, dieerfüllt. Aus der Theorie der gewöhnlichen Differentialgleichungen erhält man, dass u eindeutig gegeben ist durch u(t): = eatu0. Dies kann nun verallgemeinert werden, indem man das Problem in höheren Dimensionen betrachtet, also als Anfangswert
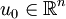 und A als eine
und A als eine  -Matrix wählt. Auch hier ist u = etAu0 die Lösung von
-Matrix wählt. Auch hier ist u = etAu0 die Lösung von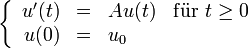 .
.
Hierbei wird die Matrixexponentialfunktion wie im Reellen durch
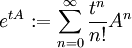 definiert. Das Cauchy-Problem kann auch auf einem Banachraum X gestellt werden, in dem
definiert. Das Cauchy-Problem kann auch auf einem Banachraum X gestellt werden, in dem 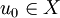 und A als ein Operator auf X gewählt wird. Ist A ein beschränkter Operator, ist u = etAu0 mit
und A als ein Operator auf X gewählt wird. Ist A ein beschränkter Operator, ist u = etAu0 mit 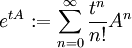 wiederum die Lösung des Cauchy-Problems. In der Anwendung vorkommende Operatoren wie der Laplace-Operator werfen die Frage nach einer Verallgemeinerung auf unstetige Operatoren auf, da in diesem Fall die Summe
wiederum die Lösung des Cauchy-Problems. In der Anwendung vorkommende Operatoren wie der Laplace-Operator werfen die Frage nach einer Verallgemeinerung auf unstetige Operatoren auf, da in diesem Fall die Summe 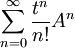 im Allgemeinen nicht konvergiert. Damit ergibt sich das Problem, wie man die Exponentialfunktion im Falle eines unbeschränkten Operators definieren soll. Unabhängig voneinander konnten Einar Hille und Kōsaku Yosida um das Jahr 1984 eine Lösung präsentieren:
im Allgemeinen nicht konvergiert. Damit ergibt sich das Problem, wie man die Exponentialfunktion im Falle eines unbeschränkten Operators definieren soll. Unabhängig voneinander konnten Einar Hille und Kōsaku Yosida um das Jahr 1984 eine Lösung präsentieren:Ansatz von Hille: Ausgehend von der im Reellen geltenden Identität
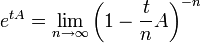 erhält man
erhält man 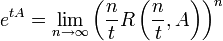 . Diese Darstellung hat den Vorteil, dass die Resolvente beschränkt ist und damit auf der rechten Seite nur beschränkte Operatoren auftauchen. Hille konnte zeigen, dass unter gewissen Umständen der Grenzwert dieser Folge existiert. Betrachtet man eine stark stetige Halbgruppe T, wie sie in der Einleitung definiert ist, mit ihrem Erzeuger A, erfüllt sie die Gleichung
. Diese Darstellung hat den Vorteil, dass die Resolvente beschränkt ist und damit auf der rechten Seite nur beschränkte Operatoren auftauchen. Hille konnte zeigen, dass unter gewissen Umständen der Grenzwert dieser Folge existiert. Betrachtet man eine stark stetige Halbgruppe T, wie sie in der Einleitung definiert ist, mit ihrem Erzeuger A, erfüllt sie die Gleichung 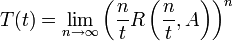 .
.Yosida-Approximation: Yosidas Idee war es, den (unbeschränkten) Operator A durch eine Folge beschränkter Operatoren zu definieren. Dazu setzte er An: = nAR(n,A) und zeigte, dass An in D(A) punktweise gegen A konvergiert. Weiterhin erzeugen An als beschränkte Operatoren stark stetige Halbgruppen Tn mit
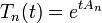 , die für jedes
, die für jedes 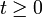 punktweise in X gegen einen Operator T(t) konvergieren. Die Familie
punktweise in X gegen einen Operator T(t) konvergieren. Die Familie 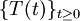 von Operatoren ist in der Tat eine stark stetige Halbgruppe, und jede stark stetige Halbgruppe kann durch die Yosida-Approximation angenähert werden.
von Operatoren ist in der Tat eine stark stetige Halbgruppe, und jede stark stetige Halbgruppe kann durch die Yosida-Approximation angenähert werden.Literatur
- Tosio Kato: Perturbation Theory for Linear Operators. 2. Auflage. Springer-Verlag 1995, ISBN 354058661X.
- Ammon Pazy: Semigroups of Linear Operators and Applications to Partial Differential Equations. Applied Mathematical Sciences 44, Springer-Verlag, Berlin 1983, ISBN 3-540-90845-5.
- Einar Hille, Ralph Phillips: Functional Analysis and Semigroups. AMS Colloquium Publications Vol. 31
- Klaus-Jochen Engel, Rainer Nagel: One-Parameter Semigroups for Linear Evolution Equations. Graduate Texts in Mathematics 194, Springer-Verlag 2000, ISBN 0387984631.
Wikimedia Foundation.