- Integralcosinus
-
Der Integralkosinus ist eine durch ein nicht elementar integrierbares Integral gegebene Funktion. Er ist definiert als:
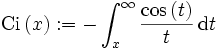 . [1]
. [1]
Es lässt sich eine überall konvergente Reihe angeben:
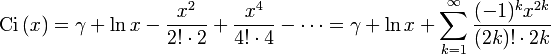 .
.
Dabei ist γ = 0,577215... die Euler-Mascheroni-Konstante.
Anmerkung: In verschiedenen Formelsammlungen wird der Integralkosinus mit umgekehrten Vorzeichen definiert.
Siehe auch
- Integralsinus
- Integraltangens
- Integralexponentialfunktion
Einzelnachweise
- ↑ HU Berlin Prof. Bank Analysis II für Physiker Seite 30 - abgegrufen am 13. März 2007
Wikimedia Foundation.
