- Integralexponentialfunktion
-
In der Mathematik ist die Integralexponentialfunktion
 als
alsdefiniert.
Da
 bei t = 0 divergiert, ist das obige Integral für x > 0 als cauchyscher Hauptwert zu verstehen.
bei t = 0 divergiert, ist das obige Integral für x > 0 als cauchyscher Hauptwert zu verstehen.Die Integralexponentialfunktion hat die Reihendarstellung
wobei ln der natürliche Logarithmus und γ die Euler-Mascheroni-Konstante ist.
Die Integralexponentialfunktion ist eng mit dem Integrallogarithmus
 verwandt, es gilt
verwandt, es giltEbenfalls eng verwandt ist eine Funktion, die über einen anderen Integrationsbereich integriert:
Diese Funktion kann als Erweiterung der Integralexponentialfunktion auf negative reelle Werte aufgefasst werden, da
Beide Funktionen können gemeinsam als ganze Funktion ausgedrückt werden:
Durch diese Funktion lassen sich die anderen beiden als
und
darstellen.
Die Integralexponentialfunktion ist Spezialfall der unvollständigen Gammafunktion
- En(x) = xn − 1Γ(1 − n,x).
Sie kann auch als
verallgemeinert werden.
Quellen
- William H. Press et al.: Numerical Recipes (FORTRAN). Cambridge University Press, New York 1989.
- Milton Abramowitz und Irene A. Stegun (Hrsg.): Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover, New York 1972. (Siehe Kapitel 5)
- R. D. Misra: Proc. Cambridge Phil. Soc. Band 36, 1940, S. 173 (Bitte überprüfen! Nach JFM zweifelhaft, befremdlicher Titel: On the stability of crystal lattices. II, p.173-182)
Weblinks
- Eric W. Weisstein: Exponential Integral. In: MathWorld. (englisch) (englisch)
- Eric W. Weisstein: En-Function. In: MathWorld. (englisch) (englisch)
Wikimedia Foundation.

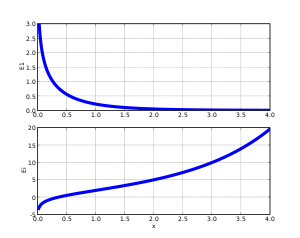
 (oben) und
(oben) und 







