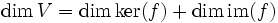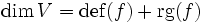Kern-Bild-Formel — Der Rangsatz oder Dimensionssatz ist ein Satz aus dem mathematischen Teilgebiet der linearen Algebra. Er zeigt einen Zusammenhang zwischen der Dimension des Bildes und der des Kerns einer linearen Abbildung f von einem Vektorraum V in einen… … Deutsch Wikipedia
Satz vom abgeschlossenen Bild — Der Satz vom abgeschlossenen Bild ist ein mathematischer Satz aus dem Teilgebiet der Funktionalanalysis. Er macht eine Aussage darüber, wann das Bild eines stetigen linearen Operators abgeschlossen ist. Inhaltsverzeichnis 1 Motivation 2 Satz vom… … Deutsch Wikipedia
Recht am eigenen Bild — Das Recht am eigenen Bild oder Bildnisrecht ist eine besondere Ausprägung des allgemeinen Persönlichkeitsrechts. Es besagt, dass jeder Mensch grundsätzlich selbst darüber bestimmen darf, ob überhaupt und in welchem Zusammenhang Bilder von ihm… … Deutsch Wikipedia
Adjungierter Operator — In der Funktionalanalysis kann zu jedem dicht definierten linearen Operator T ein adjungierter Operator (manchmal auch dualer Operator) T * definiert werden. Lineare Operatoren können zwischen zwei Vektorräumen mit gemeinsamem Grundkörper K (… … Deutsch Wikipedia
Epistemologie — Bild dessen, was ich sehe. Welche Teile dieses Bildes gehören zu „mir“, welche zur „Außenwelt“, wie leiste ich die Zuordnung? Abbildung aus Ernst Mach, Die Analyse der Empfindungen (1900), S. 15. Die Erkenntnistheorie oder Epistemologie ist neben … Deutsch Wikipedia
Epistemologisch — Bild dessen, was ich sehe. Welche Teile dieses Bildes gehören zu „mir“, welche zur „Außenwelt“, wie leiste ich die Zuordnung? Abbildung aus Ernst Mach, Die Analyse der Empfindungen (1900), S. 15. Die Erkenntnistheorie oder Epistemologie ist neben … Deutsch Wikipedia
Erkenntnisgewinn — Bild dessen, was ich sehe. Welche Teile dieses Bildes gehören zu „mir“, welche zur „Außenwelt“, wie leiste ich die Zuordnung? Abbildung aus Ernst Mach, Die Analyse der Empfindungen (1900), S. 15. Die Erkenntnistheorie oder Epistemologie ist neben … Deutsch Wikipedia
Erkenntnislehre — Bild dessen, was ich sehe. Welche Teile dieses Bildes gehören zu „mir“, welche zur „Außenwelt“, wie leiste ich die Zuordnung? Abbildung aus Ernst Mach, Die Analyse der Empfindungen (1900), S. 15. Die Erkenntnistheorie oder Epistemologie ist neben … Deutsch Wikipedia
Erkenntnistheoretiker — Bild dessen, was ich sehe. Welche Teile dieses Bildes gehören zu „mir“, welche zur „Außenwelt“, wie leiste ich die Zuordnung? Abbildung aus Ernst Mach, Die Analyse der Empfindungen (1900), S. 15. Die Erkenntnistheorie oder Epistemologie ist neben … Deutsch Wikipedia
Erkenntnistheoretisch — Bild dessen, was ich sehe. Welche Teile dieses Bildes gehören zu „mir“, welche zur „Außenwelt“, wie leiste ich die Zuordnung? Abbildung aus Ernst Mach, Die Analyse der Empfindungen (1900), S. 15. Die Erkenntnistheorie oder Epistemologie ist neben … Deutsch Wikipedia
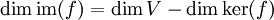berechnen kann.
