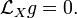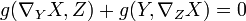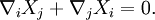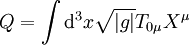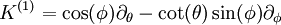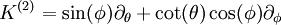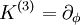Killingvektor

Ein Killing-Vektorfeld (benannt nach dem deutschen Mathematiker Wilhelm Killing) ist ein Vektorfeld auf einer riemannschen Mannigfaltigkeit, das die Metrik erhält. Killing-Vektorfelder sind die infinitesimalen Generatoren von Isometrien (siehe auch Lie-Gruppe).

Wenn die Koeffizienten von g_μν in einer Basis von dx^a unabhängig von der Ortskoordinate x^k sind, ist 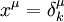$x^\mu = \delta^\mu_k$ automatisch ein Killing-Vektorfeld, wobei 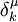$\delta^\mu_k$ das Kroneckerdelta ist.

Erklärung

Ein Vektorfeld X ist ein Killing-Vektorfeld, wenn die Lie-Ableitung der Metrik g bezüglich X verschwindet:

$\mathcal{L}_X g = 0.\,$

Drückt man dies mithilfe des Levi-Civita-Zusammenhangs aus, bedeutet dies

$g(\nabla_Y X, Z) + g(Y, \nabla_Z X) = 0$

für alle Vektoren Y und Z. In lokalen Koordinaten führt dies zur sogenannten Killing-Gleichung

$\nabla_i X_j + \nabla_j X_i = 0.$

Ein Killing-Feld ist eindeutig bestimmt durch einen Vektor an einem Punkt und seinen kovarianten Gradienten auf der ganzen Raumzeit.

Ein Vektorfeld ist genau dann ein Killing-Vektorfeld, wenn es entlang jeder Geodätischen ein Jacobi-Vektorfeld ist.

Erhaltungsgrößen

Da Killing-Vektorfelder Isometrien generieren, gibt es in der Physik zu jedem Killing-Vektorfeld eine Erhaltungsgröße der entsprechenden Raumzeit. In der allgemeinen Relativitätstheorie sind Killing-Vektorfelder daher von großer Bedeutung zur Charakterisierung von Lösungen der einsteinschen Feldgleichungen. Die Erhaltungsgröße Q zu einem Killing-Vektorfeld X berechnet sich dabei als

$Q = \int \mathrm{d}^3x \sqrt{|g|} T_{0 \mu} X^{\mu}$

wobei T der Energie-Impuls-Tensor und |g| der Betrag der Determinante des metrischen Tensors ist. In der Formel wurde die einsteinsche Summenkonvention verwendet.

Beispiel

Das Killing-Vektorfeld K⁽²⁾ auf der zweidimensionalen Einheitssphäre. In türkis sind einige Integralkurven des Vektorfeldes eingezeichnet.

Ein Satz unabhängiger Killing-Vektorfelder der Einheitssphäre S² mit der induzierten Metrik ds² = dθ² + sin²(θ)dφ² in Kugelkoordinaten sind:

$K^{(1)} = \cos(\phi)\partial_\theta - \cot(\theta)\sin(\phi)\partial_\phi$

$K^{(2)} = \sin(\phi)\partial_\theta + \cot(\theta)\cos(\phi)\partial_\phi$

$K^{(3)} = \partial_\phi$

Alle Linearkombinationen dieser Vektorfelder stellen wieder Killing-Vektorfelder dar.

Literatur

• Steven Weinberg: Gravitation and Cosmology. John Wiley & sons, New York 1972, ISBN 0-471-92567-5. 
• Jürgen Jost: Riemannian Geometry and Geometric Analysis. Springer Verlag, Berlin 2002, ISBN 3-540-42627-2. 
• Adler, Ronald; Bazin, Maurice & Schiffer, Menahem: Introduction to General Relativity. 2. Auflage. McGraw-Hill, New York 1975, ISBN 0-07-000423-4 (siehe Kapitel 2 und 9). 
• Misner, Thorne, Wheeler: Gravitation. W. H. Freeman and Company, 1973, ISBN 0-7167-0344-0.