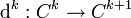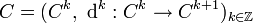- Kohomologiegruppe
-
Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion!
Die Kohomologietheorie ist ein Teilgebiet der algebraischen Topologie. Es handelt sich hierbei um das duale Konzept zur Homologietheorie.
Inhaltsverzeichnis
Definition der Kohomologiegruppe
Sei
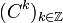 eine halbexakte Folge von abelschen Gruppen (bzw. Vektorräumen, Garben oder allgemeiner G-Torseuren) und sei
eine halbexakte Folge von abelschen Gruppen (bzw. Vektorräumen, Garben oder allgemeiner G-Torseuren) und seifür alle
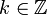 ein Gruppenhomomorphismus. Außerdem muss
ein Gruppenhomomorphismus. Außerdem muss 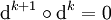 für alle
für alle 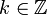 gelten. Dieser Homomorphismus heißt auch Korandoperator. Dann nennt man
gelten. Dieser Homomorphismus heißt auch Korandoperator. Dann nennt maneinen Kokettenkomplex. Eine Element aus
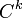 heißt k-Kokette. Gilt für eine Kokette
heißt k-Kokette. Gilt für eine Kokette 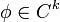 die Gleichung
die Gleichung 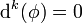 , so nennt man diese auch Kozykel. Gibt es ein
, so nennt man diese auch Kozykel. Gibt es ein 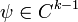 mit
mit 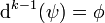 , so heißt
, so heißt 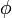 Korand. Mit
Korand. Mit 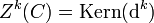 bezeichnet man die Untergruppe aller Kozykel, und analog bezeichnet man mit
bezeichnet man die Untergruppe aller Kozykel, und analog bezeichnet man mit 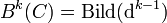 die Untergruppe aller Koränder.
die Untergruppe aller Koränder.Die k-te Kohomologiegruppe des Kokettenkomplexes
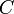 ist dann definiert als
ist dann definiert als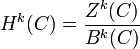 .
.
Ein Element der Kohomologiegruppe
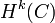 wird Kohomologieklasse genannt. Ein Kokettenkomplex heißt exakt, wenn das Bild von
wird Kohomologieklasse genannt. Ein Kokettenkomplex heißt exakt, wenn das Bild von 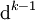 stets mit dem Kern von
stets mit dem Kern von 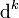 übereinstimmt. Einfach ausgedrückt misst also die Kohomologiegruppe die „Nichtexaktheit“ des Kokettenkomplexes
übereinstimmt. Einfach ausgedrückt misst also die Kohomologiegruppe die „Nichtexaktheit“ des Kokettenkomplexes 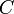 .
.Kohomologiefunktoren
Sei
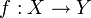 eine stetige Abbildung zwischen topologischen Räumen. Diese Abbildung induziert eine Abbildung
eine stetige Abbildung zwischen topologischen Räumen. Diese Abbildung induziert eine Abbildung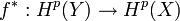 mit
mit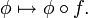
Beachte die entgegengesetze Richtung von f * im Gegensatz zu f. Diese Abbildung heißt Kohomologie-Homomorphismus und erfüllt die folgenden zwei Eigenschaften:
- Sei
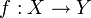 und
und 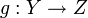 stetig, dann gilt
stetig, dann gilt  .
. - Der Homomorphismus, welcher durch die identische Abbildung induziert wird, ist wieder die identische Abbildung.
Also ist die Zuordnung
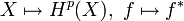 ein kontravarianter Funktor von der Kategorie der topologischen Räume in die Kategorie der abelschen Gruppen. Die Kohomologietheorie ist also das duale Konzept zur Homologietheorie, denn die Homologiefunktoren sind die entsprechenden kovarianten Funktoren.
ein kontravarianter Funktor von der Kategorie der topologischen Räume in die Kategorie der abelschen Gruppen. Die Kohomologietheorie ist also das duale Konzept zur Homologietheorie, denn die Homologiefunktoren sind die entsprechenden kovarianten Funktoren.Topologische Invarianz von Kohomologien
Sei
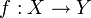 eine Homeomorphismus, dann ist für jedes
eine Homeomorphismus, dann ist für jedes 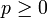
ein Isomorphismus.
Beispiele
Beispiele für Kohomologien sind die
- De-Rham-Kohomologie
- Dolbeault-Kohomologie
- Čech-Kohomologie oder Garbenkohomologie
- Motivische Kohomologie
- Étale Kohomologie
Literatur
- John M. Lee: Introduction to Topological Manifolds. Springer-Verlag, ISBN 0-387-98759-2.
Wikimedia Foundation.