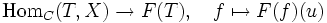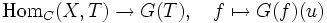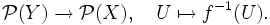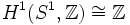Darstellbarer Funktor

Darstellbarkeit ist ein Begriff aus dem mathematischen Teilgebiet der Kategorientheorie. Es beschreibt den Umstand, dass es für gewisse Konstruktionen "klassifizierende Objekte" gibt.

Definition

Ein kontravarianter Funktor 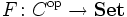$F\colon C^{\mathrm{op}}\to\mathbf{Set}$ von einer Kategorie C in die Kategorie der Mengen heißt darstellbar, wenn es ein Paar (X,u) bestehend aus einem Objekt von C und einem Element 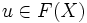$u\in F(X)$ gibt, so dass

$\mathrm{Hom}_C(T,X)\to F(T),\quad f\mapsto F(f)(u)$

für alle Objekte T von C bijektiv ist. Man schreibt dann auch einfach

F(T) = Hom_C(T,X).

Ein kovarianter Funktor 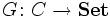$G\colon C\to\mathbf{Set}$ heißt darstellbar, wenn es ein analoges Paar (X,u) gibt, so dass

$\mathrm{Hom}_C(X,T)\to G(T),\quad f\mapsto G(f)(u)$

bijektiv ist.

Weitere Bezeichnungen:

• Für ein Element von F(T) heißt der entsprechende Morphismus 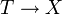$T\to X$ auch klassifizierender Morphismus.
• X heißt darstellendes Objekt, auch wenn durch X selbst die natürliche Äquivalenz

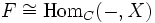$F\cong\mathrm{Hom}_C({-},X)$ bzw. $G\cong\mathrm{Hom}_C(X,{-})$

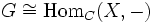
noch nicht festgelegt ist.

• u wird oft universell genannt, weil jedes Element von F(T) für irgendein Objekt T Bild von u unter F(f) mit einem geeigneten Morphismus

$f\colon T\to X$

ist. (Analoges gilt im Fall kovarianter Funktoren.)

Eigenschaften

• Wird ein kontravarianter Funktor F wie oben einerseits durch (X₁,u₁), andererseits aber auch durch X₂,u₂ dargestellt, so gibt es genau einen Isomorphismus 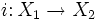$i\colon X_1\to X_2$, für den F(i)(u₂) = u₁ gilt. Er ist der klassifizierende Morphismus von 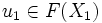$u_1\in F(X_1)$ bezüglich (X₂,u₂).
• Darstellbare Funktoren sind linksexakt, d.h.

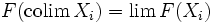$F(\mathrm{colim}\, X_i) = \lim F(X_i)$ bzw. $G(\lim X_i)=\lim G(X_i)$.

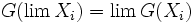Beispiele

• Die Bildung der Potenzmenge 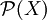$\mathcal P(X)$ einer Menge kann als kontravarianter Funktor betrachtet werden: für eine Abbildung 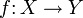$f\colon X\to Y$ von Mengen sei die induzierte Abbildung das Urbild von Teilmengen:

$\mathcal P(Y)\to\mathcal P(X),\quad U\mapsto f^{-1}(U).$

Dieser Funktor wird durch das Paar ({0,1},{1}) dargestellt wird. Die klassifizierende Abbildung einer Teilmenge 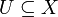$U\subseteq X$ ist die charakteristische Funktion von U.

• Die folgenden Vergißfunktoren sind darstellbar:

von	nach	dargestellt durch
Abelsche Gruppen	Mengen	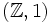$(\mathbb Z,1)$
Vektorräume über einem Körper K	Mengen	(K,1)
unitäre Ringe	Mengen	$(\mathbb Z[T],T)$
Topologische Räume	Mengen	( * , * ) (ein einpunktiger Raum)

• Ein Beispiel aus der kommutativen Algebra bilden die Kähler-Differentiale mit der universellen Derivation.
• Die Fundamentalgruppe eines punktierten topologischen Raumes ist per definitionem ein darstellbarer Funktor auf der Kategorie der punktierten topologischen Räume mit den Homotopieklassen punktierter Abbildungen als Morphismen:

π₁(X,x₀) = [(S¹, * ),(X,x₀)].

• Die erste Kohomologiegruppe 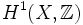$H^1(X,\mathbb Z)$ mit Koeffizienten in den ganzen Zahlen ist ein kontravarianter Funktor, der durch die 1-Sphäre S¹ zusammen mit einem der beiden Erzeuger von

$H^1(S^1,\mathbb Z)\cong\mathbb Z$

dargestellt wird. Allgemein gibt es darstellende Räume K(π,n) für die Funktoren Hⁿ( − ,π) für beliebige abelsche Gruppen π und natürliche Zahlen n. Sie heißen Eilenberg-MacLane-Räume.