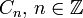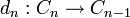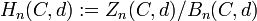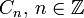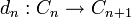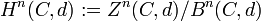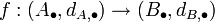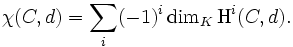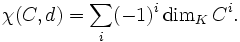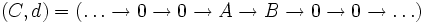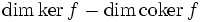Kokettenkomplex

Ein (Ko-)Kettenkomplex in der Mathematik ist eine Folge von Vektorräumen oder abelschen Gruppen oder allgemein Objekten in abelschen Kategorien, die durch Abbildungen kettenartig verknüpft sind.

Definition

Kettenkomplex

Ein Kettenkomplex besteht aus einer Folge

$\,C_n , \,n \isin \mathbb{Z}$

von Vektorräumen (abelschen Gruppen, Objekten einer abelschen Kategorie A) und einer Folge

$d_n: C_n \rarr C_{n-1}$

von linearen Abbildungen (Gruppenhomomorphismen, Morphismen in A), so dass

$\,d_n d_{n+1} = 0$

für alle n gilt. Elemente von 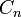$\,C_n$ heißen n-Ketten. Elemente von

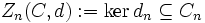$Z_n(C,d):=\ker d_n\subseteq C_n$ bzw. $B_n(C,d):=\mathop{\mathrm{im}} d_{n+1}\subseteq C_n$

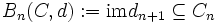
heißen n-Zykel bzw. n-Ränder. Aufgrund der Bedingung 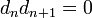$\,d_n d_{n+1}=0$ ist jeder Rand ein Zykel. Der Quotient

$\,H_n(C,d) := Z_n(C,d)/B_n(C,d)$

heißt n-te Homologiegruppe (Homologieobjekt) von 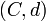$\,( C, d)$, ihre Elemente heißen Homologieklassen. Zykel, die in derselben Homologieklasse liegen, heißen homolog.

Kokettenkomplex

Ein Kokettenkomplex besteht aus einer Folge

$C_n,\, n \isin \mathbb{Z}$

von Vektorräumen (abelschen Gruppen, Objekten einer abelschen Kategorie A) und einer Folge

$\,d_n : C_n \rarr C_{n+1}$

von linearen Abbildungen (Gruppenhomomorphismen, Morphismen in A), so dass

$\,d_n d_{n-1} = 0$

für alle n gilt. Elemente von 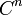$\,C^n$ heißen n-Koketten. Elemente von

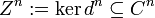$\,Z^n:=\ker d^n\subseteq C^n$ bzw. $B^n:=\mathop{\mathrm{im}} d^{n-1}\subseteq C^n$

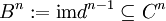
heißen n-Kozykel bzw. n-Koränder. Aufgrund der Bedingung 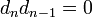$\,d_n d_{n-1} = 0$ ist jeder Korand ein Kozykel. Der Quotient

$\,H^n(C,d) := Z^n(C,d)/B^n(C,d)$

heißt n-te Kohomologiegruppe (Kohomologieobjekt) von 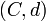$\,(C, d)$, ihre Elemente Kohomologieklassen. Kozykel, die in derselben Kohomologieklasse liegen, heißen kohomolog.

Eigenschaften

• Ein Kettenkomplex 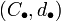$(C_\bullet,d_\bullet)$ ist genau dann exakt an der Stelle i, wenn 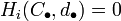$H_i(C_\bullet,d_\bullet)=0$ ist, entsprechend für Kokettenkomplexe. Die (Ko-)Homologie misst also, wie stark ein (Ko-)Kettenkomplex von der Exaktheit abweicht.

Kettenhomomorphismus

Eine Funktion

$f : (A_\bullet, d_{A,\bullet}) \to (B_\bullet, d_{B,\bullet})$

heißt (Ko)-Kettenhomomorphismus, falls sie aus einer Folge von Gruppenhomomorphismen 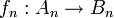$f_n : A_n \rightarrow B_n$ existiert, welche mit dem Randoperator d vertauscht. Das heißt für den Kettenhomomorphismus:

$d_{B,n} \circ f_n = f_{n-1} \circ d_{A,n}$.

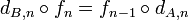Für den Kokettenhomomorphismus gilt entsprechend

$d_{B,n} \circ f_{n} = f_{n+1} \circ d_{A,n}$.

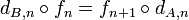Diese Bedingung stellt sicher, dass f Zykel auf Zykel und Ränder auf Ränder abbildet.

Euler-Charakteristik

Es sei (C,d) ein Kokettenkomplex aus Vektorräumen über einem Körper K. Sind nur endlich viele Kohomologiegruppen nichttrivial, und sind diese endlichdimensional, so ist die Euler-Charakteristik des Komplexes definiert als die ganze Zahl

$\chi(C,d)=\sum_i(-1)^i\dim_K\mathrm H^i(C,d).$

Sind auch die einzelnen Komponenten Cⁱ endlichdimensional und nur endlich viele von ihnen nichttrivial, so ist auch

$\chi(C,d)=\sum_i(-1)^i\dim_K C^i.$

Im Spezialfall eines Komplexes 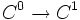$C^0\to C^1$ mit nur zwei nichttrivialen Einträgen ist diese Aussage der Rangsatz.

Beispiele

• Singuläre Homologie und Kohomologie topologischer Räume.
• Gruppen(ko)homologie.
• Jeder Homomorphismus 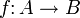$f\colon A\to B$ definiert einen Kokettenkomplex

$(C,d)=(\ldots\to0\to0\to A\to B\to0\to0\to\ldots)$

Legt man die Indizes so fest, dass sich A in Grad 0 und B in Grad 1 befindet, so ist

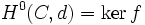$H^0(C,d)=\ker f$ und $H^1(C,d)=\mathrm{coker}\,f$.

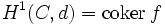Die Euler-Charakteristik

$\dim\ker f-\dim\mathrm{coker}\,f$

von (C,d) wird in der Theorie der Fredholm-Operatoren der Fredholm-Index von f genannt.

Literatur

• P. J. Hilton & U. Stammbach - A Course in Homological Algebra, Springer-Verlag, ISBN 0-387-90033-0